Ошибки анализа бывают

Классификация ошибок количественного анализа

Ошибки количественного анализа условно подразделяют на систе­матические, случайные и грубые.Грубые ошибки, обусловленные несоблюдением методики анализа, очевидны. Они устраняются при повторном проведении анализа с соблю­дением всех требуемых условий, предусмотренных методикой анализа

.А. Систематическая ошибкаРазличают: систематическую ошибку и процентную систематиче­скую ошибку.Систематическая ошибка результата анализа Д -— это статистиче­ски значимая разность между средним

х и действительным а (или ис­тинным ц) значениями содержания определяемого компонента: : ∆_о=хˉ-а или ∆_о=хˉ-μ.Систематическая ошибка результата анализа может быть больше ну­ля, меньше нуля или равна нулю.Процентная систематическая ошибка <относительная величина систематической ошибки) — это систематическая ошибка, выраженная в процентах от действительного значения а (или истинного значения μ) определяемой величины:Систематическая ошибка характеризует правильность результатов анализа; поэтому правильность анализа можно определить так же, как ка­чество анализа, отражающее близость к нулю систематической ошибки.Систематические ошибки обусловлены либо постоянно действую­щими причинами (и поэтому повторяются при многократном проведении анализа), либо изменяются по постоянно действующему закону.Источники систематических ошибок. Невозможно с исчерпываю­щей полнотой перечислить все источники систематических ошибок. Ос­новные источники систематических ошибок следующие.Методические — обусловлены особенностями методики анализа. Например, аналитическая реакция прошла не до конца; имеются потери осадка вследствие его частичной растворимости в растворе или при его промывании; наблюдается соосаждение примесей с осадком, вследствие чего масса осадка возрастает, и т. д.Инструментальные — обусловлены несовершенством используе­мых приборов и оборудования. Так, например, систематическая ошибка взвешивания на лабораторных аналитических весах составляет ±0,0002 г. Систематическая ошибка в титриметрических методах анализа вносится вследствие неточности калибровки бюреток, пипеток, мерных колб, мер­ных цилиндров, мензурок и т. д.Индивидуальные — обусловлены субъективными качествами аналити­ка. Так, например, дальтонизм может влиять на определение конечной точки титрования при визуальной фиксации изменения окраски индикатора.

Б. Случайные ошибки Случайные ошибки показывают отличие результатов параллельных определений друг от друга и характеризуют воспроизводимость анализа. Причины случайных ошибок однозначно указать невозможно. При мно­гократном повторении анализа они или не воспроизводятся, или имеют разные численные значения и даже разные знаки.Случайные ошибки можно оценить методами математической стати­стики, если выявлены и устранены систематические ошибки (или систе­матические ошибки меньше случайных).

Некоторые понятия математической статистики и их использование в количественном анализе.Случайная величина (применительно к количественному анализу) — измеряемый аналитический сигнал (масса, объем, оптическая плотность и др.) или результат анализа.Варианта — отдельное значение случайной величины, т. е. отдель­ное значение измерения аналитического сигнала или определяемого со­держания.Генеральная совокупность — идеализированная совокупность ре­зультатов бесконечно большого числа измерений (вариант) случайных величин.Относительная вероятность результатов в генеральной совокупности при выполнении химико-аналитических определений в большинстве слу­чаев описывается функцией Гаусса (распределением Гаусса).

Статистическая обработка и представление результатов количественного анализа Расчет метрологических параметров. На практике в количествен­ном анализе обычно проводят не бесконечно большое число определе­ний, а п = 5—6 независимых определений, т. е. имеют выборку (выбо­рочную совокупность) объемом 5—6 вариант. В оптимальном случае (при анализе, например, лекарственных препаратов) рекомендуется про­водить 5 параллельных определений, т. е. оптимальный рекомендуемый объем выборки п — 5.

Приведите уравнения реакций идентификации ацетата свинца. Укажите аналитические эффекты реакций, особенности их выполнения. К каким аналитическим группам относятся катион и анион, входящие в состав соли? Укажите групповой реагент, аналитический эффект при действии группового реагента.

Ацетат свинца Pв (CН₃ COO)₂

А)Pв +2 –II анал гр. Гр.реагент-HClр и ее соли→бел.творож ос

Ошибки в аналитических исследованиях

1.3.1. Оточности измерений

Часто стараются произвести измерения с наибольшей достижимой точностью, т. е. сделать ошибку измерения по возможности малой. Однако следует иметь в виду, что чем точнее мы хотим измерить, тем труднее это сде­лать. Поэтому не следует требовать от измерений большей точности, чем это необходимо для решения поставленной задачи. Для изготовления книжной полки длину досок вполне достаточно измерять с точностью до 0.5—1 см, или около 1 %; для изготовления некоторых деталей шарикоподшипников нужна точность в 0.001 мм, или около 0.01%, а при измерении длин волн спектральных линий иногда необходима точность в 10 -11 см, или около 10 -5 %. Не следует увлекаться получением излишней точности, когда она не нужна, но необходимо прилагать максимум усилий и не жалеть времени и труда для получения лишнего десятичного знака, когда это требуется. Но надо иметь в виду, что очень часто именно повышение точности измерений позволяет вскрыть новые закономерности.

Действительно, всякий закон, устанавливающий коли­чественную связь между физическими величинами, выво­дится в результате опыта, основой которого служат измерения. Он может считаться верным лишь с той сте­пенью точности, с какой выполнены измерения, положен­ные в его основу.

Так, например, существует хорошо проверенный со времен Ломоносова и Лавуазье закон сохранения ве­щества, по которому сумма масс веществ, вступающих в химическую реакцию, равна массе продуктов реак­ции. Однако при химической реакции поглощается или выделяется энергия. Вследствие этого в соответствии с теорией относительности масса продуктов реакции несколько отличается от суммы реагирующих масс. При сгорании угля это различие составляет

1 г на 3000 т угля. Чтобы заметить его, нужно произвести взвешивание с точностью до 3 . 10 – 8 0 /.

Следовательно, лишь в указанных пределах точности (3-10 -8 %) справедлив закон сохранения массы при ре­акции горения. Научившись взвешивать с такой точно­стью, мы сумели бы непосредственно обнаружить это изменение массы. Сейчас оно установлено только косвен­ным путем, так как нужной точности взвешивания мы, не достигли.

Однако при ядерных реакциях, когда количество вы­деляющейся энергии гораздо больше, изменение массы может быть относительно легко обнаружено.

В качестве другого примера можно указать, что по­вышение точности измерений плотности воды привело в 1932 г. к открытию тяжелого изотопа водорода — дей­терия, ничтожное содержание которого в обычной воде немного увеличивает ее плотность.

Точно так же проведенные Рэлеем в 1894 г. точные измерения плотности азота, выделенного из воздуха, показали, что она несколько выше плотности азота, по­лученного разложением чистого аммиака. Хотя это различие составляет всего около 5 мг/л, оно заставило пред­положить примесь к атмосферному азоту более тяжелого газа и привело Рамсая и Рэлея в 1895 г. к открытию инертного газа — аргона (о существовании этой группы газов до этого и не предполагали).

Можно было бы привести еще ряд примеров новых’ открытий, полученных в результате увеличения точности измерений. Из сказанного видно, как важно иногда стре­миться к максимальному увеличению точности. Для того чтобы этого достичь, нужно руководствоваться определен­ными правилами и приемами при производстве самих измерений и обработке полученных результатов. Хотя рекомендации в этом отношении не могут быть универ­сальными, но многие общие приемы хорошо разработаны и будут здесь изложены.

1.3.2. Типы ошибок

Правильная интерпретация результатов аналитических лабораторных методов требует определения и устранения возможных ошибок. Ошибки, возникающие при лабораторных исследованиях, делятся на случайные и систематические, искажающие в ту или другую сторону фактические результаты. Случайные ошибки возникают по многим причинам и практически не устранимы. Но эти ошибки при выведения средних значений

результатов не оказывают на них существенного влияния за счет разнонаправленности отклонений.

Систематические погрешности, в отличие от случайных, постоянны по знаку и близки по величине, обусловлены влиянием какого-либо фактора или их группы (совокупности). Систематические ошибки можно выявить и устранить.

Случайные ошибки обнаруживаются с помощью внутреннего лабораторного контроля результатов, т.е. выборочным повторным анализом, и при обнаружении неверных результатов последние заменяются.

Систематические ошибки устанавливаются путем выполнения внешнего контроля по специальным методикам. Ошибки выявляются не только путем проведения контрольных анализов конкретных проб, но и комплексной проверкой качества работы лабораторий.

Кроме того, в теории и практике измерений и обработки численной — формации выделяют грубые ошибки, которые по абсолютной величине значительно отличаются от всего числового ряда. К таким ошибкам приводят промахи, просчеты и описки.

Случайные ошибки при различных лабораторных и других иссследованиях характеризуются некоторыми общими закономерностями и терминологическими понятиями:

случайные ошибки, равные по величине и противоположные по знаку, возникают равновероятно;

малые по величине ошибки встречаются чаще, чем большие;

при данных условиях проведения анализа или измерения ни одна из

случайных ошибок не превзойдет по абсолютной величине определенного предела;

при возрастании числа точных измерений среднее арифметическое значение случайных ошибок измерения одной и тоже величины стремится к нулю.

Средняя ошибка или основная погрешность — вычисляется как среднеарифметическое из абсолютных значений всех ошибок, ее численное значение служит простейшим параметром точности измерения.

Недостатком этого параметра является то, что он сглаживает влияние больших ошибок. Для более точной оценки результатов Гayсc предложил использовать среднеквадратичное отклонение, где средняя ошибка вычисляется по обобщенной формуле

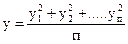(1)

где У — среднеквадратичное отклонение

п — число измерений.

Предельная ошибка. Максимальная (предельная) случайная (в отличие от грубой) ошибка для данного ряда измерений равняется утроенной среднеквадратичной.

1.3.3. Анализ ошибок

Промахи. Источником последних является не­достаток внимания экспериментатора. Для устранения промахов нужно соблюдать аккуратность и тщательность в работе и записях результатов. Иногда можно выявить промах, повторив измерение в несколько отличных усло­виях, например, перейдя на другой участок шкалы прибора. Следует иметь в виду, что многократное измерение подряд одной и той же вели-чины в одних и тех же условиях не всегда дает возмож­ность установить промах. Действительно, если при изме­рении угла наблюдатель записал 45°32’20» вместо 35°32’20», то при повторных наблюдениях он иногда будет обращать внимание только на минуты и секунды, продолжая механически записывать 45° вместо 35°. Для _того чтобы надежно установить промах, нужно либо [сместить шкалу, либо повторить измерение спустя такое время, когда наблюдатель уже забыл полученные им цифры. Разумеется, повторение измерения другим наблю-

дателем, который не знает результатов, полученных первым, почти всегда поможет вскрыть промах, если он имел место. Однако не следует считать и этот метод абсолютно надежным. Если, например, промах произошел из-за нечетко обозначенного деления шкалы (иногда путаются цифры 5 и 6 или 3 и 8), то второй наблюдатель может повторить ошибку первого. Далее будут указаны еще некоторые признаки, поз­воляющие иногда отличить промахи от закономерных результатов измерений. При всяком опыте промахи должны быть исключены, и, как уже говорилось, основной способ их устранения — особая тщательность и вни­мание во время работы.

Следует отметить, что чем удобнее условия работы и чем меньше утомлен наблюдатель, тем меньше прома­хов он делает. Поэтому желательно организовать изме­рения так, чтобы работать с комфортом, по возможности не переутомляясь и перемежая периоды снятия отсчетов с отдыхом, либо другим видом работы.

Проведение математических расчетов позволяет решить большой круг вопросов, связанных с качеством выполненных исследований. К таким вопросам относятся следующие;

выявление проб, в анализах которых допущены ошибки;

выявление анализируемых элементов или других характеристик, при определении, которых произошли ошибки;

определение знака ошибки, абсолютной и относительной ее величины;

установление уровня точности полученных результатов;

определение пределов чувствительности при работе с данным массивом проб;

выявление лабораторий, приборов или методик, использование которых привело к искажению результатов.

Случайные ошибки выявляются решением следующего выражения

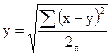(2)

где у — величина ошибки,

х — аналитическая характеристика в основных пробах,

у — аналитическая характеристика в контрольных пробах,

п — число контрольных проб.

Получив значение случайной погрешности, можно определить ее относительную величину

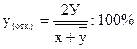(3)

где 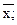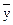— средние величины результатов в основной иконтрольной сериях анализов.

Систематические ошибки выявляются при проведении контрольных анализов, как правило, более точными методами в количествах, достаточных для статистической обработки (обычно 20 — 50 анализов). Критерием наличию ошибки служит решение неравенства:

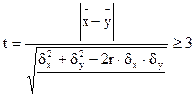(4)

где 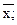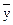— средние значения основных и контрольных анализов;

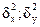— дисперсии значений определяемых величин;

r — коэффициент корреляции между величинами.

Если систематическая ошибка установлена, т.е. t≥3, то ее величина определяется решением уравнения регрессии:

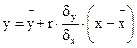(5)

Где нет возможности устранения систематической ошибки, для коррекции результатов вводят поправочный коэффициент или пересчитывает каждый анализ путем решения, приведенного уравнения.

Лекция 2. Ошибки в количественном анализе и статистическая обработка результатов анализа

Ключевые слова: параллельные определения; погрешность измерения; погрешности систематические, случайные и промахи; выборка, варианта выборки, объем выборки; среднее арифметическое; Q-критерий; размах варьирования; точность, воспроизводимость, правильность анализа; стандартное отклонение; доверительная вероятность и доверительный интервал; критерий Стьюдента; точные и приближенные числовые значения.

Любое измерение имеет свою определенную погрешность, связанную с точностью измерительной аппаратуры и особенностями метода.

Оценка погрешности результата является частью анализа. Погрешность измерения— отклонение результата измерений x_i от истинного значения измеряемой величины х_теор.

Относительная погрешность:∆_отн = (|∆_абс|/ x_теор)·100%.

По своему характеру погрешности делятся на следующие:

1. Систематические — погрешности, вызываемые причинами, действующими одинаковым образом при многократном повторении измерений (недостатки метода анализа, неисправность прибора, присутствие в реагентах веществ, мешающих определению, погрешности самого экспериментатора); их можно заранее предусмотреть, устранить или ввести на них поправку.

2. Случайные — неопределенные по величине и знаку погрешности, в появлении которых не наблюдается какой-либо закономерности. Для минимизации и численной оценки этих погрешностей анализ повторяют несколько раз, т.е. проводят параллельные (повторные) определения – измерения одной и той же величины для одной аналитической пробы в одинаковых условиях.

Совокупность результатов параллельных измерений называют выборкой. Сами результаты называют вариантами выборки. Число вариант, составляющих выборку, называют объемом выборки. На основе параллельных измерений рассчитывают среднее арифметическое –сумму вариант, деленную на объем выборки n:

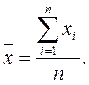
Грубые погрешности(промахи) – отдельные значения, резко отличающиеся от остальных и, как правило, полученные в условиях грубого нарушения аналитической методики. Промахи выявляют среди серии результатов повторных измерений, как правило, с помощью Q-критерия. Для его расчета результаты параллельных определений выстраивают в ряд по возрастанию их значений: х1, х2, х3,…, хn-1, хn. Сомнительным обычно является первый или последний результат в этом ряду. Q-критерий вычисляют как отношение взятой по абсолютной величине разности сомнительного результата и ближайшего к нему в ряду к разности последнего и первого в ряду. Разность хn — х1 называют размахом варьирования.

.

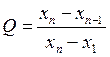Для выявления промаха рассчитанное для него Q сравнивают с табличным критическим значением Q_табл, приведенным в аналитических справочниках. Если Q Q_табл, то сомнительный результат исключают из рассмотрения, считая промахом. Промахи должны быть выявлены и устранены.

Значения Q-критерия для различной доверительной вероятности P и числа измерений n приведены в таблице:

Химический анализ характеризуется правильностью и воспроизводимостью, которые определяют его точность. Близкие значения определяемой величины в параллельных опытах говорят о воспроизводимости результатов. Если полученное среднее значение близко к истинному, то говорят о правильности результатов анализа.

Количественно воспроизводимость характеризуют стандартным отклонением S, определяемым методами математической статистики:

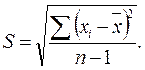
Стандартное отклонение S показывает, на какую в среднем величину отклоняются результаты n измерений от среднего значения. Кроме того, для оценки погрешности результата рассчитывают стандартное отклонение среднего арифметического:

Используя данные величины, оценивают диапазон значений, в котором с заданной вероятностью Р может находиться результат. Эта вероятность Р называется доверительной вероятностью (статистической надежностью). Обычно принимают Р=95%. Соответствующий данной вероятности интервал значений — доверительный интервал:

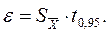
При расчетах используют специальный t_α — критерий Стьюдента, определяющий ширину доверительного интервала, в котором может находиться результат анализа. Значения t_α-критерия находят в специальных таблицах, учитывая число измерений и степень вероятности α (0,95 или 0,99) нахождения результатов анализа в данном доверительном интервале. Например, для α = 0,95 значения t_α-критерия в зависимости от числа измерений n равны:

Представление полученного результата с доверительным интервалом: .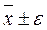

Числовые значения подразделяют на точные и приближенные. Значащими цифрами числа называют все его цифры, кроме нулей, стоящих слева до первой отличной от нуля цифры. Нули, стоящие в середине и в конце числа, являются значащими. Например, в числе 427,205 — 6 значащих цифр; 0,00365 — 3 значащие цифры; 244,00 — 5 значащих цифр.

Каждый результат анализа не может быть точнее, чем это позволяют измерительные приборы. Допустимое расхождение результатов параллельных определений обычно регламентируется ГОСТ, ОСТ или ТУ на конкретный анализ. В количественном химическом анализе применяют аналитические весы (погрешность взвешивания не более 0,0002 г) и мерную посуду, измеряющую объемы с точностью до сотых долей миллилитра. Считается, что при взвешивании на аналитических весах погрешность приблизительно равна 0,02%, при точном измерении объемов – 0,2%. Если погрешность вычислений не оговорена заранее, то следует иметь в виду, что точная концентрация вычисляется до 4-й значащей цифры, точная масса — до 4-го десятичного знака после запятой, точная массовая доля (процентное содержание) — до сотых долей. Если значащих цифр указано меньше, то значение является приближенным.

Контрольные вопросы

1. Что такое погрешность измерения? Как классифицируют погрешности?

2. Что такое параллельные определения, выборка, варианта и объем выборки?

3. Дайте определение промаха. Как его можно выявить?

4. Охарактеризуйте параметры, определяющие точность анализа.

5.Какие количественные параметры математической статистики используются для представления результата анализа?

6. Какие числовые значения являются точными, а какие приближенными? 7. Какие цифры являются значащими?

Список рекомендуемой литературы

1. Васильев В.П. Аналитическая химия. Кн. 1. Титриметрические и гравиметрический методы анализа. — М.: Дрофа, 2005. — С. 24 — 49.

2. Харитонов Ю.Я. Аналитическая химия (аналитика): учебник для вузов. В 2 кн. Кн. 2. Количественный анализ. Физико-химические (инструментальные) методы анализа. – М.: Высшая школа, 2001. – С. 7 — 25.

С.Б. Денисова, О.И. Михайленко

Лекция 3. Титриметрический анализ. Основные понятия и термины

Ключевые слова: титриметрические методы анализа, титрование, титрант (рабочий раствор), точка эквивалентности, растворы приготовленные и установленные, первичный стандарт (исходное вещество), фиксанал (стандарт-титр), индикатор, скачок титрования, конечная точка титрования, индикаторная ошибка.

Количественные методы анализа, основанные на точном измерении объема реагента точно известной концентрации, израсходованного на реакцию с определяемым веществом, называют титриметрическими. Титрование — процесс постепенного добавления раствора реагента точно известной концентрации (титранта, рабочего раствора, стандартного раствора) к определяемому веществу до момента, при котором количество титранта эквивалентно количеству определяемого вещества, то есть до точки эквивалентности. Достижение точки эквивалентности можно определить:

1) с помощью индикатора – специального реактива, обладающего способностью изменять свою окраску при изменении концентрации определяемого вещества вблизи точки эквивалентности;

2) безындикаторным способом — визуально по резкому изменению какого-либо видимого свойства системы (появление, изменение или исчезновение окраски, образование или растворение осадка);

3) с помощью инструментальных методов (наблюдая за изменением оптической плотности, рН, потенциала электрода, силы тока и др.).

Выбор индикатора осуществляют: а) по методу построения кривых титрования либо б) по методу расчета индикаторной ошибки.

Кривая титрования выражает графическую зависимость изменения какого-либо свойства системы (рН, потенциал и др.) от объема добавленного титранта. При этом на кривой титрования имеются области плавного (до и после точки эквивалентности) и резкого (вблизи точки эквивалентности) изменения свойства системы. Резкое изменение свойства называется скачком титрования. Границы скачка устанавливаются с точностью 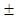0,1 % оттитрованности, что соответствует погрешности титриметрического анализа. Момент, при котором заканчивается титрование с выбранным индикатором, называют конечной точкой титрования. Даже при правильно выбранном индикаторе теоретически рассчитанная точка эквивалентности не совпадает с практически установленной конечной точкой титрования. Это приводит к возникновению индикаторной ошибки.

В зависимости от способа получения различают рабочие растворы приготовленные и установленные. Растворы, полученные по точной навеске вещества, называют приготовленными. Вещество, по точной навеске которого можно непосредственно приготовить рабочий раствор, называют первичным стандартом (исходным веществом); к нему предъявляется ряд требований:

1) вещество должно быть химически чистым; 2) состав вещества должен точно соответствовать формуле; 3) вещество должно быть устойчивым при хранении как в твердом виде, так и в растворе; 4) должно быть хорошо растворимо и 5) должно иметь возможно большую молярную массу эквивалента. Кроме того, рабочие растворы могут быть приготовлены из фиксаналов (стандарт-титров) — запаянных ампул с количеством вещества, необходимым для приготовления 1 л точно 0,1 или 0,01 н. раствора.

Если вещество не отвечает требованиям к первичному стандарту, то по его навеске готовят раствор с примерно желаемой концентрацией, которую точно устанавливают в процессе титрования раствора с точно известной концентрацией. Такие растворы называют установленными. Концентрация этих растворов, как правило, с течением времени меняется, поэтому ее необходимо проверять через определенные промежутки времени (1-3 недели).

Для титриметрических определений можно использовать реакции раз-личных типов, но все они должны удовлетворять следующим требованиям:

1. Реакции должны проходить быстро, а состояние равновесия наступать практически мгновенно.

2. Реакции должны протекать до конца и количественно.

3. Реакции должны протекать стехиометрически, посторонние продукты не должны мешать титрованию.

4. Должен иметься способ фиксирования точки эквивалентности.

Методы титриметрического анализа классифицируют по типу реакций, лежащих в основе определения веществ:

ЭТАПЫ КОЛИЧЕСТВЕННОГО ХИМИЧЕСКОГО АНАЛИЗА;

Классификация ошибок количественного анализа.

Ошибки количественного анализа условно подразделяют на систематические, случайные и грубые.

Грубые ошибки, обусловленные несоблюдением методики анализа, очевидны. Они устраняются при повторном проведении анализа с соблюдением всех требуемых условий, предусмотренных методикой анализа.

а) Систематическая ошибка

Различают: систематическую ошибку и процентную систематическую ошибку.

Систематическая ошибка результата анализа Δ — это статистически значимая разность между средним х–и действительным а(или истинным μ) значениями содержания компонента:

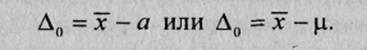
Систематическая ошибка результата анализа может быть больше нуля, меньше нуля или равна нулю.

Процентная систематическая ошибка (относительная величина систематической ошибки) — это систематическая ошибка, выраженная в процентах от действительного значения а(или истинного значения μ) определяемой величины:

δ = (х–– а)∙100% / а или δ = (х–– μ)•100% / μ (1.3)

Для относительной величины систематической ошибки вместо сим­вола 5 используют также обозначение Δ %.

Систематическая ошибка характеризует правильность результатов анализа; поэтому правильность анализа можно определить так же, как качество анализа, отражающее близость к нулю систематической ошибки.

Систематические ошибки обусловлены либо постоянно действующими причинами (и поэтому они повторяются при многократном проведении анализа), либо изменяются по постоянно действующему закону, который можно учесть.

Так, например, процентная систематическая ошибка (Δс/с)•100% фотометрических определений (с — концентрация, Δс — систематическая ошибка определения концентрации фотометрическим методом) минимальна в интервале изменений оптической плотности А от А ≈ 0,2 до А ≈ 0,8 и составляет (Δс/с)•100%

Существуют способы выявления систематических ошибок.

а) Использование стандартных, образцов. Общий состав стандартного образца должен быть близким к составу анализируемой пробы, а содержание определяемого компонента в стандартном образце должно быть точно известно.

Анализ стандартного образца — наиболее надежный способ выявления наличия или отсутствия систематической ошибки и оценки правильности результата анализа.

б) Анализ исследуемого объекта другими методами. Исследуемый объект анализируют методом или методами, которые не дают систематической ошибки (метрологически аттестованы), и сравнивают результаты анализа с данными, полученными при анализе того же объекта с использованием оцениваемой методики или не аттестованного оборудования. Сравнение позволяет охарактеризовать правильность оцениваемой методики анализа.

в) Метод добавок или метод удвоения — используют при отсутствии стандартных образцов и метрологически аттестованной методики (метода) анализа.

Анализируют образец, используя оцениваемую методику. Затем удваивают массу анализируемой пробы или увеличивают (уменьшают) массу в иное число раз, снова находят содержание определяемого компонента в уже новой пробе и сравнивают результаты анализов. Должна выполняться определенная закономерность (например, пропорциональность).

б) Случайные ошибки.

Случайные ошибки показывают отличие результатов параллельных определений друг от друга и фактически характеризуют воспроизводимость анализа. Причины случайных ошибок однозначно указать невозможно. При многократном повторении анализа они или не воспроизводятся, или имеют разные численные значения и даже разные знаки.

Случайные ошибки можно оценить методами математической статистики, если выявлены и устранены систематические ошибки (или систематические ошибки меньше случайных).

Наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности называется метрологией. Количественный химический анализ, целью которого является определение содержания веществ в разных объектах, может рассматриваться как измерительная процедура, характеризующаяся рядом специфических особенностей.

Количественный химический анализ, прежде всего, является многостадийным процессом, включающим ряд этапов и стадий. При выполнении химического анализа с помощью любого мето­да можно выделить следующие основные этапы:

— постановка аналитической задачи;

— выбор метода анализа;

— оценка качества анализа;

— принятие решений по результатам анализа.

При постановке аналитической задачи необходимо дать характеристику объекта анализа, указать химическую формулу определяемого компонента, возможный интервал его содержаний, требуемую точность и продолжительность анализа.

Выбор метода анализа определяется поставленной аналитической задачей и техническими возможностями аналитической лаборатории.

Этап, связанный непосредственно с проведением химического анализа, наиболее трудоемок и включает ряд стадий, представленных на рис. 5.2.

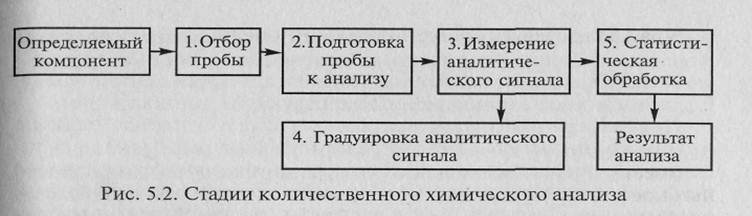
Методика анализа включает подробное описание последовательности и условий проведения всех стадий анализа. Точное следование методике анализа позволяет выполнить анализ с минимальными погрешностями на каждой стадии и получить правильный результат анализа.

Первая стадия химического анализа — отбор средней (представительной) пробы. Это небольшая часть анализируемого объекта, средний состав и свойства которой должны быть идентичны во всех отношениях среднему составу и свойствам объекта анализа. Содержание определяемого компонента в анализируемой пробе должно отражать среднее содержание этого компонента во всем исследуемом объекте, т. е. анализируемая проба должна быть представительной. Погрешность в отборе пробы часто определяет общую погрешность химического анализа. Не оценив погрешность на этой стадии, нельзя говорить о правильности определения компонента в анализируемом объекте.

Подготовка пробы к анализу включает ряд сложных операций, например, такие как высушивание пробы, разложение (вскрытие) пробы, устранение влияния мешающих компонентов. В зависимости от цели анализа, природы объекта и выбранного метода могут быть использованы разные модификации и комбинации этих операций. В правильном проведении химического анализа роль подготовки пробы настолько велика, что химик-аналитик должен каждый раз оценивать необходимость включения операций пробоподготовки в методику анализа, их влияние на общую погрешность анализа.

После отбора и подготовки пробы наступают стадии химического анализа, на которых определяют количество компонента. С этой целью измеряют аналитический сигнал. В большинстве методов им является среднее из измерений физической величины на заключительной стадии анализа, функционально связанной с содержанием определяемого компонента. Это может быть сила тока, ЭДС системы, оптическая плотность, интенсивность излучения и т.д. В отдельных методах анализа возможно непосредственное определение содержания. Например, в гравиметрическом методе иногда прямо измеряют массу определяемого компонента.

При определении количества компонента измеряют величину аналитического сигнала. Затем рассчитывают содержание компонента с использованием функциональной зависимости аналитического сигнала от содержания: у = f(с), которая устанавливается расчетным или опытным путем и может быть представлена в виде формулы, таблицы или графика. Содержание может быть выражено абсолютным количеством определяемого компонента в молях, в единицах массы или через соответствующие концентрации.

При измерении аналитического сигнала учитывают наличие полезного аналитического сигнала, являющегося функцией содержания определяемого компонента, и аналитического сигнала фона, обусловленного примесями определяемого компонента и мешающими компонентами в растворах, растворителях и матрице образца, а также «шумами» в измерительных приборах, усили­телях и другой аппаратуре. Эти шумы не имеют отношения к опре­деляемому компоненту, но накладываются на его собственный аналитический сигнал. Задача аналитика состоит в том, чтобы максимально снизить величину аналитического сигнала фона и, главное, сделать минимальными его колебания.

Обычно аналитический сигнал фона учитывают в контрольном (холостом) опыте, когда через все стадии химического анализа проводится проба, не содержащая определяемого компонента. Полезным при этом будет аналитический сигнал, равный разности измеренного сигнала и аналитического сигнала фона.

На основании существующей зависимости между аналитическим сигналом и содержанием находят концентрацию определяе­мого компонента. Обычно при этом используют методы градуированного графика, стандартов или добавок. Описанные в литературе другие способы определения содержания компонента, как правило, являются модификацией этих трех методов.

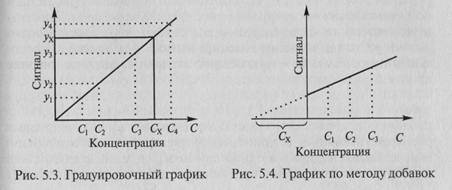
Наиболее распространен метод градуировочного графика: в координатах (аналитический сигнал – содержание компонента) строят график с использованием образцов сравнения с разными и точно известными уровнями содержания компонента (концентрация С). Затем, измерив величину аналитического сигнала в пробе, находят содержание определяемого компонента по градуировочному графику (рис. 5.3).

В методе стандартов измеряют аналитический сигнал в образ­це сравнения (стандартном образце) с известным содержанием компонента и в анализируемой пробе: У_ст = sС_ст и у_х = sС_Х, где s-коэффициент пропорциональности.

Если определенное в идентичных условиях значение s заранее известно, то можно провести расчет по формуле С_х = У_х/S. Обычно же используют соотношение У_ст/У_Х = С_ст/С_Х, откуда

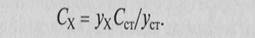
Иногда работают с двумя стандартными образцами, в которых содержание компонента отличается от предполагаемого содержания в анализируемой пробе в одном случае в меньшую, в другом — в большую сторону. Этот вариант метода стандартов называют методом ограничивающих растворов. Содержание определяемого компонента рассчитывают по формуле

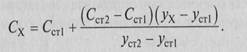
Если при определении малых количеств компонента нужно учесть влияние матрицы образца на величину аналитического сигнала, то часто используют методы добавок — расчетный или графический.

При определении содержания расчетным методом берут две аликвоты раствора анализируемой пробы. В одну из них вводят добавку определяемого компонента известного содержания. В обеих пробах измеряют аналитический сигнал — у_х и у_х+доб—

Неизвестную концентрацию определяемого компонента рас­считывают по формуле

где V_доб и С_доб — объем и концентрация добавленного раствора определяемого компонента; V — аликвота анализируемой пробы.

При определении содержания компонента графическим методом берут п аликвот анализируемой пробы: 1, 2, 3, . п. Во 2-ю, . п-ю аликвоты вводят известные, возрастающие, количества опре­деляемого компонента. Во всех аликвотах измеряют аналитический сигнал и строят график в координатах аналитический сигнал -содержание определяемого компонента, приняв за условный нуль содержание определяемого компонента в аликвоте без добавки (аликвота 1). Экстраполяция полученной прямой до пересечения с осью абсцисс дает отрезок слева от условного нуля координат, величина которого в выбранном масштабе и единицах измерения соответствует С_х определяемого компонента (рис. 5.4).

Метод стандартов и метод добавок применимы для линейной градуировочной функции. Метод градуировочного графика допускает использование как линейной, так и нелинейной функций анали­тический сигнал—содержание. В последнем случае требуется боль­шее число экспериментальных данных, и результат определения содержания компонента бывает, как правило, менее точным.