Первичный анализ данных

Первичный анализ данных эмпирического исследования

В процессе анализа и обработки эмпирических данных обычно используются такие термины как “признак”, “показатель”, “параметр”, “переменная”. Употребляются они чаще всего как синонимы. Другой смысл имеет термин “значение”. Значение — это определенная числовая величина того или иного показателя, выявленная у конкретного испытуемого (Куликов, 2001).

Обработка полученных эмпирических данных начинается обычно с первичного анализа переменных. Для большей наглядности изображения они заносятся в таблицы или изображаются в виде графиков. Проверка точности выполнения этой части работы обеспечивает достоверность дальнейшей обработки и анализа результатов исследования.

Использование методов математической статистики при обработке первичных эмпирических данных необходимо для повышения достоверности выводов, как в научном, так и в практическом психологическом исследовании. Начинает исследователь обычно с анализа первичных статистик. Важнейшими среди них являются:

1. средняя арифметическая

6. среднее квадратичное отклонение.

Типичными задачами математической обработки данных являются:

1. оценка достоверности различий,

2. корреляционный анализ,

3. факторный анализ,

4. анализ изменчивости признаков.

1. Во многих исследованиях осуществляется поиск различий в психологических показателях у испытуемых, характеризующихся разными особенностями. Для обработки соответствующих данных могут использоваться критерии на выявлении различий в уровне исследуемого признака или в распределении признака.

2. Во многих исследованиях осуществляется поиск взаимосвязи психологических показателей у одних и тех же испытуемых. Для обработки соответствующих данных могут использоваться коэффициенты корреляции.

3. Для выявления структуры данных (и соответственно структуры изучаемой психологической реальности), а также взаимосвязи данных, используется факторный анализ.

4. Во многих исследованиях интерес представляет анализ изменчивости признака под влиянием каких-либо контролируемых факторов, или другими словами, оценка влияния разных факторов на изучаемый признак. Во психологических исследованиях может выявляться значимость изменений (сдвига) каких-либо психологических, поведенческих параметров и проявлений за определенный промежуток времени, в определенных условиях (например, в условиях коррекционного воздействия). Формирующие эксперименты в практической психологии решают именно эту задачу. Для обработки соответствующих данных могут использоваться коэффициенты для оценки достоверности сдвига в значениях исследуемого признака.

Для выбора статистических критериев и знакомства с основами их применения для обработки эмпирических данных можно использовать ряд пособий (например, Гласс, Стенли, 1976; Закс, 1976; Рунион, 1982; Сидоренко, 2001). Каждый исследователь предпочитает статистические критерии, исходя из типа задачи и вида данных, которые подлежат обработке.

При выборе математико-статистического критерия нужно, прежде всего, идентифицировать тип переменных (признаков) и шкалу, которая использовалась при измерении психологических показателей и других переменных – например, возраст, состав семьи, уровень образования. В качестве переменных могут выступать любые показатели, которые можно сравнивать друг с другом (то есть измерять). Это может быть время выполнения задания, количество ошибок, уровень самооценки, количество правильно решенных задач и качественные особенности их выполнения, личностные показатели, получаемые в психологических тестах, и другие. В области практической психологии широко используются номинативные и порядковые шкалы. Речевые высказывания клиента, виды поведенческих реакций, улыбки, взгляды, – все это может рассматриваться в качестве переменных. Главное — иметь четкие и ясные критерии их отнесения к тому или иному типу в зависимости от поставленных гипотез и задач.

При выборе математико-статистического критерия нужно ориентироваться также на тип распределения данных, который получился в исследовании.

Параметрические критерии используются обычно в том случае, когда распределение полученных данных рассматривается как нормальное. Нормальное распределение с большей вероятностью (но не обязательно) получается при выборках более 100 испытуемых (может получиться и при меньшем количестве, а может не получиться и при большем). При использовании параметрических критериев необходима проверка нормальности распределения.

Для непараметрических критериев тип распределения данных не имеет значения. При небольших объемах выборки испытуемых, часто используемых в психологии, целесообразно использовать непараметрические критерии, которые дают большую достоверность выводам, независимо от того, получено ли в исследовании нормальное распределение данных. В некоторых случаях статистически обоснованные выводы могут быть сделаны даже при выборках в 5-10 испытуемых.

Выбор метода математической обработки полученных эмпирических данных очень важная и ответственная часть исследования. Это учитывается в процессе планирования исследования. Заранее продумывается, какие эмпирические данные будут регистрироваться, с помощью каких методов будут обрабатываться, и какие выводы при разных результатах обработки можно будет сделать. При этом учитываются ограничения, которые имеет каждый критерий в его использовании. Если данные не подходят по каким-либо причинам под выбранный критерий, то ищут какой-либо другой критерий (возможно изменив тип представления этих данных).

Процедура обработки данных и вычисления статистического критерия проводится “вручную” или с использованием статистической программы персонального компьютера. Для компьютерной обработки наиболее популярными среди психологов программами являются SPSS и Statistica.

Методы математической обработки данных используются и для анализа результатов практической психологической работы исследовательского типа. Для обоснования эффективности проведенной практической работы используются конкретные психологические и поведенческие показатели испытуемых “до” и “после” проведенной работы. Применение математико-статистических критериев для проверки значимости изменений придаст большую доказательность выводам работы.

Первичная статистическая обработка данных

Лабораторная работа №3. Статистическая обработка данных в системе MatLab

Общая постановка задачи

Основной целью выполнения лабораторной работы является ознакомление с основами работы со статистической обработкой данных в среде MatLAB.

Теоретическая часть

Первичная статистическая обработка данных

Статистическая обработка данных основывается на первичных и вторичных количественных методах. Цель первичной обработки статистических данных является структурирование полученных сведений, подразумевающее группировку данных в сводные таблицы по различным параметрам. Первичные данных должны быть представлены в таком формате, чтобы человек смог провести приближенную оценку полученной совокупности данных и выявить информацию о распределении данных полученной выборки данных, например, однородность или компактность данных. После первичного анализа данных применяются методы вторичной статистической обработки данных, на основании которых определяются статистические закономерности в имеющемся наборе данных.

Проведение первичного статистического анализа над массивом данных позволяет получить знания о следующем:

— Какое значение наиболее характерно для выборки? Для ответа на данный вопрос определяются меры центральной тенденции.

— Велик ли разброс данных относительно этого характерного значения, т. е. какова «размытость» данных? В данном случае определяются меры изменчивости.

Стоит отметить тот факт, что статистические показатели меры центральной тенденции и изменчивостиопределяются только на количественных данных.

Меры центральной тенденции– группа величин, вокруг которых группируются остальные данные.Таким образом, меры центральной тенденции обобщают массив данных, что делает возможным формирование умозаключений как о выборке в целом, так и проведение сравнительного анализа разных выборок друг с другом.

Допустим имеется выборка данных 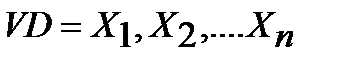, тогда меры центральной тенденции оцениваются следующими показателями:

1. Выборочное среднее– это результат деления суммы всех значений выборки на их количество.Определяется по формуле (3.1).

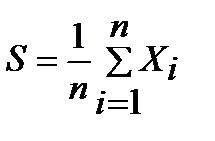(3.1)

где 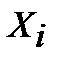— i-й элемент выборки;

n – количество элементов выборки.

Выборочное среднее позволяет получить наибольшую точность в процессе оценки центральной тенденции.

Допустим имеется выборка из 20 человек. Элементами выборки являются сведения о среднем ежемесячном доходе каждого человека. Предположим, что 19 человек имеют средний ежемесячный доход в 20 т.р. и 1 человек с доходом в 300 т.р. Суммарный ежемесячный доход всей выборки составляет 680 т.р. Выборочное среднее в данном случае S=34.

2. Медиана– формирует значение, выше и ниже которого количество отличающихся значений одинаково, т. е. это центральное значение в последовательном ряду данных. Определяется в зависимости четности/нечетности количества элементов выборке по формулам (3.2) или (3.3).Алгоритм оценки медианы для выборки данных :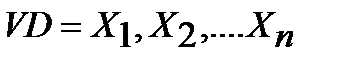

— Первым делом данные ранжируются (упорядочиваются) по убыванию/возрастанию .

— Если в упорядоченной выборке нечетное число элементов, то медиана совпадает с центральным значением.

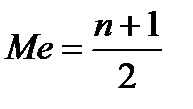(3.2)

где n — количество элементов выборки.

— В случае четного числа элементов медиана определяется как как среднее арифметическое двух центральных значений.

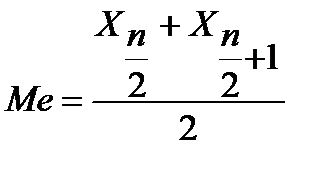(3.3)

где — средний элемент упорядоченной выборки;

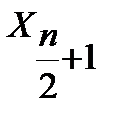— элемент упорядоченной выборки следующий за ;

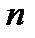— количество элементов выборки.

-В том случае, если все элементы выборки различны, то ровно половина элементов выборки больше медианы, а другая половина меньше. Например, для выборки <1, 5, 9, 15, 16>медиана совпадает с элементом 9.

В статистическом анализе данных медиана позволяет определить элементы выборки, которые сильно влияют на значение выборочного среднего.

Допустим имеется выборка из 20 человек. Элементами выборки являются сведения о среднем ежемесячном доходе каждого человека. Предположим, что 19 человек имеют средний ежемесячный доход в 20 т.р. и 1 человек с доходом в 300 т.р. Суммарный ежемесячный доход всей выборки составляет 680 т.р. Медиана, после упорядочивания выборки, определяется как среднеарифметическое десятого и одиннадцатого элементов выборки) и равняется Ме=20 т.р. Данный результат интерпретируется следующим образом: медиана делит выборку на две группу, таким образом, что можно сделать заключение о том, что в первой группе у каждого человека средний ежемесячный доход не более 20 т.р., а во второй группе не менее 20 т.р. В данном примере можно говорить о том, что медиана характеризуется тем, сколько зарабатывает «средний» человек. В то время как значение выборочного среднего значительно превышено S=34, что указывает на неприемлемость данной характеристики при оценке среднего заработка.

Таким образом, чем больше различие между медианой и выборочным средним, тем больший разброс данных выборки (в рассмотренном примере, человек с заработком в 300 т.р. явно отличается от среднестатистических людей конкретной выборки и оказывает существенное влияние на оценку среднего дохода). Что делать с подобными элементами решается в каждом индивидуальном случае. Но в общем случае для обеспечения достоверности выборки они изымаются, так как оказывают сильное влияние на оценку статистических показателей.

3. Мода (Мо) – формирует значение, наиболее часто встречающееся в выборке, т. е. значение с наибольшей частотой.Алгоритм оценки моды:

-В том случае, когда выборка содержит элементы, встречающиеся одинаково часто, то говорят, что мода в подобной выборке отсутствует.

— Если два соседних элемента выборки имеют одинаковую частоту, являющуюся больше частоты остальных элементов выборки, то мода определяется как среднее этих двух значений.

— Если два элемента выборки имеют одинаковую частоту, являющуюся больше частоты остальных элементов выборки, и при этом данные элементы не являются соседними, то говорят, что в данной выборке две моды.

Мода в статистическом анализе используется в ситуациях, когда необходимо проведение быстрой оценки меры центральной тенденции и не требуется высокая точность. Например, моду (по показателю размер либо бренд) удобно применять для определения одежды и обуви, которая пользуется наибольшим спросом у покупателей.

Меры разброса (изменчивости)– группа статистических показателей, характеризующих различия между отдельными значениями выборки. Основываясь на показателях мер разброса можно оценивать степень однородности и компактности элементов выборки. Меры разброса, характеризуются следующим набором показателей:

1. Размах — это интервал между максимальным и минимальным значениями результатов наблюдений (элементов выборки). Показатель размаха указывает на разброс значений в совокупности данных. Если размах большой, то значения в совокупности сильно разбросаны, в противном случае (размах небольшой) говорится о том, что значения в совокупности лежат близко друг к другу. Размах определяется по формуле (3.4).

(3.4)

Где 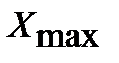— максимальный элемент выборки;

— минимальный элемент выборки.

2.Среднее отклонение– среднеарифметическая разница (по абсолютной величине) между каждым значением в выборке и ее выборочным средним. Среднее отклонение определяется по формуле (3.5).

(3.5)

где 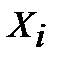— i-й элемент выборки;

— значение выборочного среднего, рассчитанное по формуле (3.1);

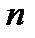— количество элементов выборки.

Модуль 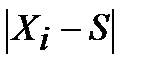необходим в связи с тем, что отклонения от среднего по каждому конкретному элементу могут быть как положительными так и отрицательными. Следовательно, если не взять модуль, то сумма всех отклонений будет близка к нулю и невозможно будет судить о степени изменчивости данных (скученности данных вокруг выборочного среднего). При проведении статистического анализа могут быть взяты мода и медиана вместо выборочного среднего.

3. Дисперсия — мера рассеяния, описывающая сравнительное отклонение между значениями данных и средней величиной. Вычисляется как сумма квадратов отклонений каждого элемента выборки от средней величины. В зависимости от размера выборки дисперсия оценивается разными способами:

— для больших выборок (n>30) по формуле 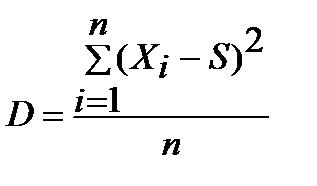(3.6)

(3.6)

Первичный статистический анализ

Невозможно предложить один алгоритм анализа данных для разных работ, но некоторые замечания сделать необходимо. Начинать надо с анализа каждой переменной в отдельности, а затем, комбинируя, сопоставляя переменные различным образом, пытаться обнаружить какие-либо закономерности. Самая распространенная ошибка студентов на этапе обработки данных – это то, что они забывают все пройденное в курсе «Математические методы в психологии». Поэтому первое, что необходимо сделать – найти тетрадь с лекциями или взять учебник из предложенных в списке литературы.

Забегая вперед, заметим, что уже сейчас, проводя первичную обработку своих данных, вы готовитесь к их интерпретации при написании основного текста работы. Обсуждение полученных данных в тексте всегда (!) начинается с их описания.Описание должно быть предельно строгим, т.е. содержать в себе только факты с их качественными (есть – нет) или количественными характеристиками. Количественные (статистические) характеристики должны быть перед обсуждением наглядно представлены: таблицы, диаграммы, гистограммы, графики и т.д. Обсуждение результатов корреляционного анализа (см. далее) должно сопровождаться демонстрацией коэффициентов корреляции с их уровнем значимости и, по возможности, корреляционных плеяд. В обсуждении результатовраскрывается значение полученных фактов с точки зрения теории – той теоретической концепции, которая была положена в основу исследования. Самое, пожалуй, трудное здесь – это обратный перевод количественных (и качественных) параметров, характеристик и фактов на язык психологических понятий и конструктов. Корректный перевод можно осуществить только, если хорошо представляешь содержательный смысл того или иного статистического параметра. Таким образом, данные в тексте даются в последовательности: наглядное представление – описание – обсуждение – доказательство/опровержение гипотезы.

Для автоматизированного подсчета первичных статистик используйте также программу «STATISTIKA». Обращаемся к Basic Statistics and Tables и далее Descriptive statistics (описательная статистика) и Frequency tables (частотное распределение). Если у вас выведены ваши данные, тогда на панели выбираете Analysis, и откроется окно со списком основных статистических операций, которые необходимо будет использовать при обработке данных.

Теперь обратимся к очень важному способу описания и представления данных – частотному распределению.

Частотное распределение или распределение частот представляет собой таблицу или график, в которых указано сколько раз встречается то или иное значение признака. Такой способ анализа и представления данных часто применяется при обработке, например, анкет, чтобы увидеть, сколько испытуемых выбирает тот или иной вариант ответа. Кстати, частотный способ описания данных один из самых любимых студентами, просто они об этом не подозревают и, следовательно, применяют его некорректно. В чем же ваши ошибки?

Рассмотрим пример разбора данных, часто встречающийся в дипломных работах студентов-психологов. У вас есть результаты методики, в которой измеряемая переменная принимает значения в номинативной шкале: низкий, средний, высокий уровень, — и двадцать испытуемых. Предположим, что ваши испытуемые дали следующие результаты. У семи испытуемых низкий результат, у одиннадцати – средний и у двух – высокий. Тогда текст чаще всего выглядит так: «Низкий результат имеют 35% испытуемых, средний – 55%, а высокий – только 10%». Вообще проценты – самая любимая студентами форма записи результата. При этом забывается, что % — это сотаячасть количества, и, если выборка существенно меньше ста, выражение части через проценты не имеет смысла.

Если выборка небольшая, то лучше просто указывать число испытуемых, получивших то или иное значение признака. А перед тем как анализировать переменную, ее распределение лучше дать таблицей, при этом вместо процентов указывать относительную частоту встречаемости всех значений признака. Например, так как сделано в таблице 5. Если какое-либо значение не встречается, то частота f=0 все равно должна быть указана. В таблице 5 объединены три методики, дающие номинативное распределение признака, и четыре группы испытуемых. (Данные взяты из дипломной работы Балышевой Н.А.). При описании таблицы мы можем сравнивать как признаки, так и группы между собой. Помимо этого, последняя строка дает общее по всем группам распределение признаков, и сразу можно видеть, что по первой методике преобладающие результаты высокие, а по двум другим средние.

Что касается графического представления частотного распределения, можно использовать как полигоны частот, гистограммы, диаграммы и др. формы представления. Так гистограмма, выполненная в «STATISTIKA», будет выглядеть следующим образом (см. рис.1, пример 3 из раздела «интерпретация корреляционного анализа»). Гистограмма используется только для количественных переменных, когда значение признака представимо числом. Если этого сделать нельзя, можно использовать обычную столбиковую диаграмму

Анализ данных. Доказательство исследовательских гипотез

Типовые задачи, которые решают психологи при обработке эмпирического материала, следующие:

1. Сопоставление групп испытуемых по какому-либо признаку для выявления различий между ними по этому признаку.

2. Сопоставление того, что было “до” с тем, что стало “после” экспериментальных или “формирующих” воздействий.

3. Сопоставление эмпирического распределения значений признака с каким-либо теоретическим законом или с другим эмпирическим распределением, чтобы доказать неслучайность различия в распределениях.

4. Сопоставление двух признаков на одной выборке для установления степени согласованности их изменений, их сопряженность, корреляцию между ними.

5. Сопоставление индивидуальных значений, полученных при разных комбинациях условий, чтобы выявить характер взаимодействия этих условий и их влияние на индивидуальное значение признака.

Каждая из приведенных задач на этапе планирования требовала определенных условий проведения исследования, и также на этапе обработки данных требует определенных критериев доказательности. Прежде всего, вы должны ответить на следующие вопросы:

1. Какого качества моя выборка?

2. Какое обобщение в отношении результатов мне потребуется?

В соответствие с ответами вы будете выбирать математическую модель. Вообще-то эти проблемы уже должны были быть решены на этапе планирования исследования и проведения пилотажа. Но для студенческих работ такая дальновидность не характерна: вопросы математической обработки данных оставляются на самый конец работы над дипломом. Что касается пилотажа, да еще с обработкой, он представляет собой исключение, большую редкость в дипломах психологов.

Итак, если объем выборки:

n ≤ 30, то выборка малая,

30 200, то выборка большая.

В психологических студенческих работах чаще встречаются выборки первая или вторая с n

Полезные статьи → Статистические методы анализа данных в решении практических задач (часть первая)

Опрос сотрудников, клиентов, потребителей, – это не просто сбор информации, а полноценное исследование. А целью всякого исследования является научно обоснованная интерпретация изученных фактов. Первичный материал необходимо обработать, а именно упорядочить и проанализировать. После опроса респондентов происходит анализ данных исследования. Это ключевой этап. Он представляет собой совокупность приемов и методов, направленных на то, чтобы проверить, насколько были верны предположения и гипотезы, а также ответить на заданные вопросы. Данный этап является, пожалуй, наиболее сложным с точки зрения интеллектуальных усилий и профессиональной квалификации, однако позволяет получить максимум полезной информации из собранных данных. Методы анализа данных многообразны. Выбор конкретного метода зависит, в первую очередь, от того, на какие вопросы мы хотим получить ответ. Можно выделить два класса процедур анализа:

• одномерные (дескриптивные) и
• многомерные.

Целью одномерного анализа является описание одной характеристики выборки в определенный момент времени. Рассмотрим более подробно.

Одномерные типы анализа данных

Количественные исследования

Дескриптивный анализ

Дескриптивные (или описательные) статистики являются базовым и наиболее общим методом анализа данных. Представьте, что вы проводите опрос с целью составления портрета потребителя товара. Респонденты указывают свой пол, возраст, семейное и профессиональное положение, потребительские предпочтения и т.д., а описательные статистики позволяют получить информацию, на основе которой будет строиться весь портрет. В дополнение к числовым характеристикам создаются разнообразные графики, помогающие визуально представить результаты опроса. Всё это многообразие вторичных данных объединяется понятием «дескриптивный анализ». Полученные в ходе исследования числовые данные наиболее часто представляются в итоговых отчетах в виде частотных таблиц. В таблицах могут быть представлены разные виды частот. Давайте рассмотрим на примере: Потенциальный спрос на товар

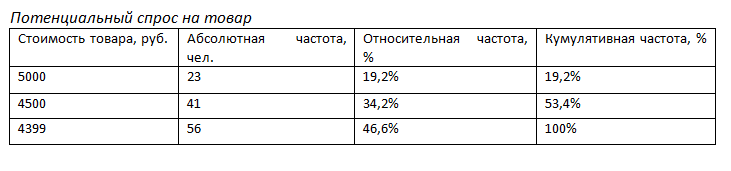
1. Абсолютная частота показывает, сколько раз тот или иной ответ повторяется в выборке. Например, 23 человека купили бы предложенный товар стоимостью 5000 руб., 41 человек – стоимостью 4500 руб. и 56 человек – 4399 руб.
2. Относительная частота показывает, какую долю данное значение составляет от всего объема выборки (23 человека – 19,2%, 41 – 34,2%, 56 – 46,6%).
3. Кумулятивная или накопленная частота показывает долю элементов выборки, не превышающих определенное значение. Например, изменение процента респондентов, готовых приобрести тот или иной товар при уменьшении цены на него (19,2% респондентов готовы купить товар за 5000 руб., 53,4% — от 4500 до 5000 руб., и 100% — от 4399 до 5000 руб. ).

Наряду с частотами, дескриптивный анализ предполагает расчет различных описательных статистик. Соответствуя своему названию, они предоставляют основную информацию о полученных данных. Уточним, использование конкретной статистики зависит от того, в каких шкалах представлена исходная информация. Номинальная шкала используется для фиксации объектов, не имеющих ранжированного порядка (пол, место жительства, предпочитаемая марка и т.д.). Для подобного рода массива данных нельзя рассчитать каких-либо значимых статистических показателей, кроме моды — наиболее часто встречающегося значения переменной. Несколько лучше в плане анализа ситуация обстоит с порядковой шкалой. Здесь становится возможным, наряду с модой, расчет медианы – значения, разбивающего выборку на две равные части. Например, при наличии нескольких ценовых интервалов на товар (500-700 руб. руб., 700-900, 900-1100 руб.) медиана позволяет установить точную стоимость, дороже или дешевле которой потребители готовы приобретать или, наоборот, отказаться от покупки. Наиболее богатыми на все возможные статистики являются количественные шкалы, которые представляют собой ряды числовых значений, имеющих равные интервалы между собой и поддающихся измерению. Примерами подобных шкал могут служить уровень дохода, возраст, время, отводимое на покупки и т.д. В данном случае становятся доступными следующие информационные меры: среднее, размах, стандартное отклонение, стандартная ошибка среднего. Конечно, язык цифр является довольно «сухим» и для многих весьма непонятным. По этой причине дескриптивный анализ дополняется визуализацией данных путем построения различных диаграмм и графиков, как, например: гистограммы, линейные, круговые или точечные диаграммы.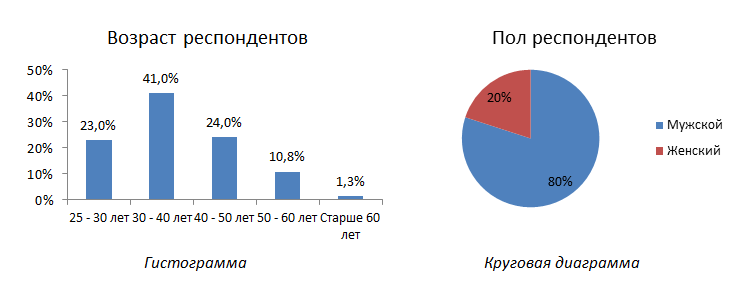

Таблицы сопряженности и корреляции

Таблицы сопряженности – это средство представления распределения двух переменных, предназначенное для исследования связи между ними. Таблицы сопряженности можно рассматривать как частный тип дескриптивного анализа. В них также является возможным представление информации в виде абсолютных и относительных частот, графическая визуализация в виде гистограмм или точечных диаграмм. Наиболее эффективно таблицы сопряженности проявляют себя в определении наличия взаимосвязи между номинальными переменными (например, между полом и фактом потребления какого-либо продукта). В общем виде таблица сопряженности выглядит так. Зависимость между полом и пользованием страховыми услугами

Статистический анализ данных

На основе представленных в таблице данных и можно делать выводы о наличии/отсутствии взаимосвязи между исследуемыми переменными. Для более точного выявления наличия связи между переменными используют разные статистические критерии. Наиболее часто применяются такие, как:

• критерий Хи-квадрат (χ2);
• коэффициент сопряженности;
• критерий лямбда;
• коэффициент R Спирмена;
• критерий корреляции Пирсона и др.

Правильный выбор критерия является решающим шагом для получения корректных результатов. Поэтому, если перед вами стоит задача проведения статистического анализа и интерпретация его результатов, но вы не чувствуете уверенности – лучше обратиться к специалистам сервиса Анкетолог, чтобы не получить неправильные выводы, не приближающие к решению проблемы.

По вопросам расчета индексов:

Телефон: +7 (383) 203-49-99

Продолжение статьи «Статистические методы анализа данных для решения практических задач»: часть вторая и часть третья.