Метод анализа иерархий является методом
Метод анализа иерархий
Назначение . С помощью онлайн-калькулятора производятся вычисление коэффициентов важности для элементов каждого уровня — индексы однородности и отношения однородности.
- Решение онлайн
- Видеоинструкция
- Оформление Word
Таблица 2. Шкала отношений
Теорема 1 . В положительной обратносимметрической квадратной матрице λmax≥n.
Теорема 2 . Положительная обратносимметрическая квадратная матрица А согласованна тогда и только тогда, когда λmax=n.
Таким образом, для оценки однородности суждений эксперта можно использовать отклонение величины максимального собственного значения λmax от порядка матрицы n.
Согласованность суждения оценивается индексом однородности (индексом согласованности) или отношением однородности (отношением согласованности) в соответствии со следующими формулами:
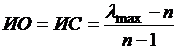
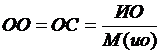
M(ио) — среднее значение индекса однородности случайным образом составленной матрицы парных сравнений, которое основано на экспериментальных данных. Значение есть табличная величина, входным параметром выступает размерность матрицы (таблица 6).
Таблица 6. Среднее значение индекса однородности в зависимости от порядка матрицы
Пример . Рассмотрим матрицу парных сравнений и вычислим приближенное значение главного собственного вектора:

Просуммируем элементы каждой строки и найдем сумму всех элементов матрицы: 

Нормализуя вектор Ws делением каждой координаты на величину S, получаем приближенное значение главного собственного вектора:

Приближенное значение максимального собственного значения можно найти по формуле λmax=e T AW, рассмотренной выше:

При таком вычислении главного собственного вектора и максимального собственного значения может оказаться, что согласованная в действительности матрица является несогласованной по вычислениям и наоборот.
Пример . Вычислим отношение согласованности рассматриваемой выше матрицы, взяв в качестве максимального собственного значения его точное и приближенное число. 



При большей погрешности метода вычисления главного собственного вектора, отношение согласованности матрицы парных сравнений могло оказаться больше 0.01 .
Желательно использовать процедуры точного нахождения собственных значений и векторов матриц. Такое пожелание превращается в требование в особо ответственных задачах.
Пример (из книги Т. Саати). Рассмотрим общее благополучие индивидуума – высший уровень иерархии. На этот уровень в основном влияют детские, юношеские и взрослые впечатления. Факторы развития и зрелости, отражающиеся в благополучии, могут включать как влияние отца и матери в отдельности, так и их совместное влияние как родителей, социоэкономический фон, отношения с братьями и сестрами, группу ровесников, школьное обучение, религиозный статус и т.д.
На перечисленные выше факторы, которые составляют второй уровень иерархии, влияют соответствующие критерии. Например, влияние отца может быть разбито на категории, включающие его темперамент, строгость, заботу и привязанность. Отношение с братьями и сестрами можно дальше характеризовать их количеством, разницей в возрасте, полом; моделирование воздействия и роли ровесников обеспечивает более яркую картину влияния друзей, обучения в школе и учителей.
В качестве альтернативной основы описания для второго уровня можно включить чувство собственного достоинства, уверенность в будущем, адаптируемость к новым людям и новым обстоятельствам и т.д., влияющих или находящихся под влиянием расположенных выше элементов.
Более полная основа психологической предыстории может включать несколько сотен элементов на каждом уровне, выбранных экспертами и расположенных таким образом, чтобы получить максимальное понимание рассматриваемого индивидуума.
Рассмотрим ограниченный случай, где испытуемый чувствует, что уверенность в его силы подорвана и его социальная приспособляемость ослаблена запретами в детстве. Ему задают вопросы только о детских впечатлениях и просят попарно установить связь между следующими элементами на каждом уровне.
Построим иерархию, в которой: ОБ – общее благополучие; Д – чувство собственного достоинства; У – чувство уверенности в будущем; А – способность адаптироваться к другим; П – явная привязанность, проявленная по отношению к субъекту; Э – идеи строгости, этики; Н – действительное наказание ребенка; Л – подчеркивание личной приспособляемости к другим; М – влияние матери; О – влияние отца; Р – влияние обоих родителей.

Рисунок 1 — Иерархическая схема общего благополучия индивидуума
 WОБ=(0.701; 0.193; 0.106), λmax=3.26; ИС=0.07; OC=0.12
WОБ=(0.701; 0.193; 0.106), λmax=3.26; ИС=0.07; OC=0.12
 WД=(0.604; 0.213; 0.064; 0.119), λmax=4.35; ИС=0.12; OC=0.13
WД=(0.604; 0.213; 0.064; 0.119), λmax=4.35; ИС=0.12; OC=0.13
 WУ=(0.604; 0.213; 0.064; 0.119), λmax=4.35; ИС=0.12; OC=0.13
WУ=(0.604; 0.213; 0.064; 0.119), λmax=4.35; ИС=0.12; OC=0.13
 WA=(0.127; 0.281; 0.120; 0.463), λmax=5.42; ИС=0.47; OC=0.52
WA=(0.127; 0.281; 0.120; 0.463), λmax=5.42; ИС=0.47; OC=0.52
 WП=(0.721; 0.210; 0.069), λmax=4; ИС=0.33; OC=0.57
WП=(0.721; 0.210; 0.069), λmax=4; ИС=0.33; OC=0.57
 WЭ=(0.333; 0.333; 0.333), λmax=3; ИС=0.0; OC=0.0
WЭ=(0.333; 0.333; 0.333), λmax=3; ИС=0.0; OC=0.0
 WН=(0.713; 0.061; 0.176), λmax=3.11; ИС=0.06; OC=0.10
WН=(0.713; 0.061; 0.176), λmax=3.11; ИС=0.06; OC=0.10
 WЛ=(0.701; 0.097; 0.202; 0.463), λmax=3.14; ИС=0.07; OC=0.12
WЛ=(0.701; 0.097; 0.202; 0.463), λmax=3.14; ИС=0.07; OC=0.12
Осуществим иерархический синтез:

Индивидууму посоветовали больше общаться с отцом с целью уравновешивания влияния родителей.
В приведенном примере некоторые матрицы несогласованные. Однако следует понимать, что человеку в данной ситуации нельзя было повторно задавать одни и те же вопросы до тех пор, пока все матрицы не стали бы однородными.
После решения задачи синтеза иерархии, оценивается однородность всей иерархии с помощью суммирования показателей однородности всех уровней, приведенных путем взвешивания к первому иерархическому уровню.
Метод анализа иерархий: особенности и область применимости
Этот метод, разработанный Т. Саати, применяется при решении многих проблем, таких как:
· Определение приоритетных направлений научных исследований;
· Проектирование сложных технических систем;
· Планирование развития фирм;
· Прогнозирование цен на продукцию;
· Выбор новых информационных систем или прикладных программ конкурирующих производителей.
В общем случае иерархия определяет расположение некоторых объектов (элементов иерархии) в порядке от высшего к низшему, от старшего к младшему по степени подчиненности (Рис. 15.2).
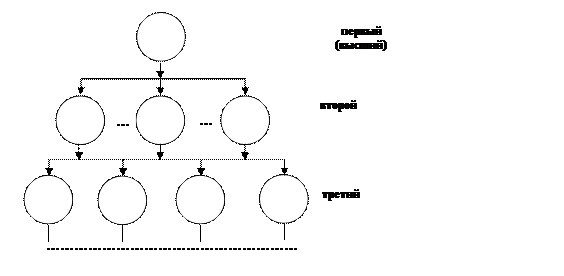
Рис. 15.2. Схематическое изображение иерархии.
Метод анализа иерархий включает:
· иерархическое структурирование проблемы;
· попарное сравнение элементов иерархии;
· поэтапное выявление приоритетов.
Высший уровень соответствует цели проблемы. Элементы последующих уровней могут отождествляться:
· с возможными решениями (альтернативами);
· со сторонами, заинтересованными в том или ином решении проблемы;
· с показателями (критериями) эффективности и т.п.
Простейшей является трехуровневая иерархия, включающая (Рис. 15.3):
· уровень цели – первый уровень
· уровень альтернатив (возможных решений) – второй уровень;
· уровень критериев – третий уровень.
Иногда в качестве второго уровня рассматривается уровень критериев, а в качестве третьего – уровень альтернатив.
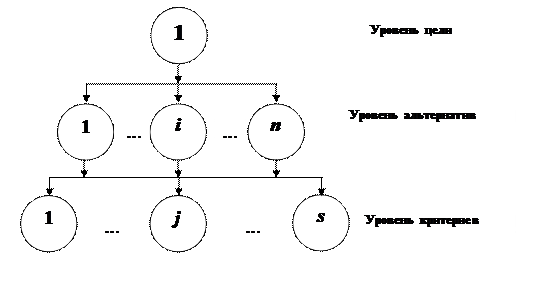
Рис. 15.3. Простейшая трехуровневая иерархия.
Пример. Менеджер отбирает одного из трех претендентов на вакантную должность на основании следующих критериев: 1) возраст, 2) образование, 3) владение информационными технологиями, 4) знание иностранного языка, 5) коммуникабельность, 6) психологическая устойчивость, 7) способность к самообучению. Здесь иерархия является трехуровневой: число элементов второго уровня (уровня альтернатив) равно трем, а третьего (уровень критериев) — семи.
При структурировании проблемы необходимо соблюдать ряд требований:
Ø Все элементы одного уровня должны быть попарно сравнимы. Это позволяет выявить предпочтения среди альтернатив и определить наилучшее решение.
Ø Структурирование проблемы производится совместно всеми заинтересованными лицами для полноты перечня возможных решений и отражения всего спектра точек зрения и предпочтений участников.
Ø Число элементов на любом уровне иерархии не должно превышать 7 – 9, иначе затрудняется сопоставление элементов иерархии между собой, усложняется получение взаимосогласованных оценок и возрастает риск получения ошибочных решений.
Пример. Решается вопрос о закупке технологической линии для производства компьютеров. Основными критериями выбора для менеджера являются стоимость и производительность линии, причем относительную важность (вес) производительности он оценивает в 17% (0,17), а стоимости — в 83% (0,83). Рассматривается возможность покупки линий трех конкурирующих производителей 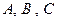 . Оценка линий этих производителей путем попарных сравнений с точки зрения интересующих менеджера критериев дает следующий результат:
. Оценка линий этих производителей путем попарных сравнений с точки зрения интересующих менеджера критериев дает следующий результат:
Лекция 6. Метод анализа иерархий (метод )

Лекция 6. Метод анализа иерархий (метод )
Метод анализа иерархий (МАИ) состоит в декомпозиции проблемы на более простые составные части и дальнейшей обработке последовательности суждений эксперта по парным сравнениям. Метод анализа иерархий служит для обоснования принятия решений в условиях определенности и многокритериальности.
Метод базируется на следующих принципах.
Принцип декомпозиции. Данный принцип предусматривает структурирование проблемы в виде иерархии, что является первым этапом применения МАИ. Иерархия считается полной, если каждый элемент заданного уровня связан со всеми элементами последующего уровня. Простейшая полная иерархия проблемы многокритериального выбора включает в себя три уровня (рис. 1): цель, критерии, альтернативы.

Рис.1. Иерархия проблемы
Принцип сравнительных суждений. Чтобы установить приоритеты критериев и получить оценки для альтернативных решений, в МАИ используется метод парных сравнений — строятся матрицы парных сравнений  , где
, где  ,
,  -– «вес» i-того элемента иерархии.
-– «вес» i-того элемента иерархии.
Очевидно, что  (то есть диагональные элементы матрицы равны 1, матрица является обратносимметричной).
(то есть диагональные элементы матрицы равны 1, матрица является обратносимметричной).
По каждой матрице определяется вектор локальных приоритетов и вычисляется индекс согласованности мнений эксперта.
Принцип синтеза приоритетов. Итак, будем считать, что построены матрицы парных сравнений: одна для второго уровня иерархии (для критериев), а на каждом последующем уровне – столько матриц парных сравнений, сколько элементов содержит предшествующий уровень иерархии. Вычислены векторы локальных приоритетов по каждой матрице.
Приоритеты синтезируются, начиная со второго уровня иерархии сверху вниз. Локальные приоритеты альтернатив умножаются на приоритеты соответствующих критериев предшествующего уровня и суммируются по каждому элементу в соответствии с критериями. Таким образом, итоговой оценкой альтернативы в методе парных сравнений является вес альтернативы, вычисляемый как свертка весовых коэффициентов критериев (локальных критериев) всех уровней иерархии.
Алгоритм МАИ включает в себя следующие этапы:
1. формирование иерархии целей;
2. определение приоритетов;
3. расчет локальных векторов приоритетов;
4. проверка экспертных оценок на непротиворечивость (вычисление индекса согласованности);
5. расчет приоритетов целей и мероприятий для иерархии в целом на основе синтеза локальных приоритетов.
Рассмотрим эти этапы и проиллюстрируем их на примере.
Предприятию необходимо заключить договор о поставке товара либо с посредником 1, либо с посредником 2, либо с предприятием-изготовителем, либо с посредником 3. Выбор необходимо осуществить, оценив следующие факторы:
- цена товара (руб.); объем партий товара (шт.); место расположения поставщика (км); возможность сбоя поставок (кол-во); сроки поставок (мес.); транспортные расходы (руб.).
В таблице 1 приведены исходные данные для эксперта, на основе анализа которых он строит матрицы парных сравнений.
Таблица 1. Исходные данные
Объем партий товара
Место расположения поставщика
в течение 2 месяцев
Этап 1. Формирование иерархии целей. Производится декомпозиция проблемы принятия решений с выделением главных целей, подцелей и различных целевых функций (альтернатив). Элементы одинаковых уровней должны быть сопоставимы друг с другом с точки зрения возможности установления приоритетов.
Воспользовавшись методом Саати для решения данной проблемы, следует, в первую очередь, четко определить потенциальные выгоды, которые необходимо учитывать. Допустим, что в результате получены следующие иерархии выгод (рис. 2).

Рис. 2. Иерархия проблемы выбора поставщика
Критерии всех уровней иерархии в методе анализа иерархий должны иметь общую направленность (либо положительную, либо отрицательную), то есть либо оцениваются выгоды (доход, прибыль), либо издержки.
Этап 2. Определение приоритетов. Чтобы установить приоритеты критериев, получить оценки для альтернативных решений в МАИ используется метод парных сравнений: строятся матрицы парных сравнений  . Элемент aij матрица парных сравнений является результатом измерения по фундаментальной шкале степени предпочтительности альтернативы Ai по отношению к альтернативе Aj.
. Элемент aij матрица парных сравнений является результатом измерения по фундаментальной шкале степени предпочтительности альтернативы Ai по отношению к альтернативе Aj.
Следует помнить, что между собой сравниваются элементы принадлежащие к одному уровню иерархии, сравнение происходит по степени их соответствия конкретному элементу вышестоящего уровня. При построении матриц парных сравнений пользуются фундаментальной шкалой предпочтений (шкалой относительной важности) (табл. 2).
Количество ответов экспертов для построения матрицы парных сравнений для n альтернатив равно n*(n-1)/2 или n2/2 –n/2. При заполнении матрицы парных сравнений достаточно определить элементы, расположенные над главной диагональю матрицы. Элементы под диагональю согласно свойству обратной симметричности матрицы вычисляются по формуле  .
.
Таблица 2. Фундаментальная шкала предпочтений (шкала относительной важности)
Метод анализа иерархий: особенности и область применимости
Этот метод, разработанный Т. Саати, применяется при решении многих проблем, таких как:
· Определение приоритетных направлений научных исследований;
· Проектирование сложных технических систем;
· Планирование развития фирм;
· Прогнозирование цен на продукцию;
· Выбор новых информационных систем или прикладных программ конкурирующих производителей.
В общем случае иерархия определяет расположение некоторых объектов (элементов иерархии) в порядке от высшего к низшему, от старшего к младшему по степени подчиненности (Рис. 15.2).

Рис. 15.2. Схематическое изображение иерархии.
Метод анализа иерархий включает:
· иерархическое структурирование проблемы;
· попарное сравнение элементов иерархии;
· поэтапное выявление приоритетов.
Высший уровень соответствует цели проблемы. Элементы последующих уровней могут отождествляться:
· с возможными решениями (альтернативами);
· со сторонами, заинтересованными в том или ином решении проблемы;
· с показателями (критериями) эффективности и т.п.
Простейшей является трехуровневая иерархия, включающая (Рис. 15.3):
· уровень цели – первый уровень
· уровень альтернатив (возможных решений) – второй уровень;
· уровень критериев – третий уровень.
Иногда в качестве второго уровня рассматривается уровень критериев, а в качестве третьего – уровень альтернатив.

Рис. 15.3. Простейшая трехуровневая иерархия.
Пример. Менеджер отбирает одного из трех претендентов на вакантную должность на основании следующих критериев: 1) возраст, 2) образование, 3) владение информационными технологиями, 4) знание иностранного языка, 5) коммуникабельность, 6) психологическая устойчивость, 7) способность к самообучению. Здесь иерархия является трехуровневой: число элементов второго уровня (уровня альтернатив) равно трем, а третьего (уровень критериев) — семи.
При структурировании проблемы необходимо соблюдать ряд требований:
Ø Все элементы одного уровня должны быть попарно сравнимы. Это позволяет выявить предпочтения среди альтернатив и определить наилучшее решение.
Ø Структурирование проблемы производится совместно всеми заинтересованными лицами для полноты перечня возможных решений и отражения всего спектра точек зрения и предпочтений участников.
Ø Число элементов на любом уровне иерархии не должно превышать 7 – 9, иначе затрудняется сопоставление элементов иерархии между собой, усложняется получение взаимосогласованных оценок и возрастает риск получения ошибочных решений.
Пример. Решается вопрос о закупке технологической линии для производства компьютеров. Основными критериями выбора для менеджера являются стоимость и производительность линии, причем относительную важность (вес) производительности он оценивает в 17% (0,17), а стоимости — в 83% (0,83). Рассматривается возможность покупки линий трех конкурирующих производителей 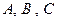 . Оценка линий этих производителей путем попарных сравнений с точки зрения интересующих менеджера критериев дает следующий результат:
. Оценка линий этих производителей путем попарных сравнений с точки зрения интересующих менеджера критериев дает следующий результат:


 , где
, где  ,
,  -– «вес» i-того элемента иерархии.
-– «вес» i-того элемента иерархии.
