Рисковая структура процентных ставок

Рисковая структура процентных ставок

Рисковая структура процентных ставок рассматривается для облигаций с одним и тем же сроком погашения. Такие облигации обладают меньшей доходностью, если уровень риска по ним меньше, если они более ликвидны или если к ним применяется льготное налогообложение. [c.170]

Точно так же существует и рисковая структура процентных ставок. При одном и том же 1 роке погашения другие факторы — характеристики кредитного риска, уровня ликвидности и налогового режима — делают некоторые финансовые инструменты более рискованными, чем остальные. Типичным примером служит то, что ценная бумага с более высоким кредитным риском имеет более высокую рыночную процентную ставку. [c.688]

Если процентная ставка по федеральным фондам г°= 0,08, то временная и рисковая структуры процентных ставок, предполагающие определенную форму и положение кривых доходности, покажут, что процентная ставка по 6-месячным казначейским ценным бумагам будет равна 0,07 (7%). [c.689]

Предположим, как показано на рис. 25-10, что равновесная однодневная процентная ставка по федеральным фондам (г.), которая определяется на рынке банковских резервов, равна 0,08 (8%). До тех пор пока временная и рисковая структуры, описываемые примерными кривыми доходности на рис. 25-10, сохраняются, 6-месячную процентную ставку по казначейским ценным бумагам можно определить, проведя перпендикуляр из точки, соответствующей 6-месячному сроку погашения на оси абсцисс, до пересечения с графиком и найдя соответствующую ординату точки пересечения. Следовательно, процентная ставка по 6-месячным казначейским ценным бумагам, которая согласуется с временной и рисковой структурами процентных ставок, равна 0,07 (7%). [c.690]

При такой ставке по федеральным фондам совокупный спрос и предложение резервов равны 77 () = 15 млрд. долл. Рисунок 25-11Б представляет собой копию рис. 25-10 он покапывает временную и рисковую структуру процентных ставок по федеральным фондам и казначейским ценным бумагам. Как и рис. 25-10, рис. 25-115 показывает, что долгосрочная (6-месячная) процентная ставка по казначейским ценным бумагам равна / » = 0,07. Наконец, рис. 25-11В представляет собой график спроса на деньги в экономике, описанный в главе 20. Если предположить, что 6-месячная процентная ставка по казначейским ценным бумагам есть адекватная процентная ставка для определения равновесного спроса на деньги, то можно увидеть, что, согласно рис. 25-11В, при г = 0,07 спрос на деньги равен Л/() = 900 млрд. долл., т. е. этот объем является равновесной денежной массой в экономике. [c.690]

Определение равновесной денежной массы. Как показано на рис. А, равновесная процентная ставка по федеральным фондам, г° = 0,08, определена равновесием на рынке банковских резервов. При заданных временной и рисковой структурах процентных ставок, представленных на рис. Б, равновесная номинальная процентная ставка по 6-месячным казначейским ценным бумагам равна л° = 0,07. Если это процентная ставка, соответствующая спросу небанковского сектора на номинальные денежные остатки (М), то рис. В показывает, что равновесный спрос на деньги равен М0 = 900 млрд. долл. [c.691]

Мы знаем, что рисковая структура процентных ставок связывает кривую доходности казначейских ценных бумаг с кривой доходности федеральных фондов. Предположив, что рисковая структура неизменна (вполне законное предположение), получаем, что кривая доходности казначейских ценных бумаг тоже смещается вниз, как показано рис. 25-12Б, вслед за покупкой аутрайт ценных бумаг со стороны ФРС. Следовательно, процентная ставка на долгосрочные ценные бумаги падает с /-° до г1 (рис. 25-12Б). [c.693]

Так же как и при таргетировании процентной ставки по федеральным фондам, зависимость между процентными ставками и денежными агрегатами играла важную роль в связывании мер денежно-кредитной политики ФРС с денежной массой. Рисунок 25-1 «7.6 показывает, что в среднем номинальная процентная ставка по казначейским ценным бумагам, согласующаяся с заданной ФРС денежной массой, равна / » Более того, временная и рисковая структуры процентных ставок (рис. 25-15Б) показывают, что процентная ставка по федеральным фондам, согласующаяся в среднем с заданной денежной массой, будет rf. Поэтому если ФРС требуется достичь именно заданной денежной массы М , то ей придется осуществить операции на открытом рынке, направленные на достижение уровня незаимствованных резервов, при котором устанавливается равновесная процентная ставка по федеральным фондам (/у). [c.700]

Что означает в данном случае риск Здесь речь не идет о классификации рискованности заемщика. (Например, предоставление кредита правительству менее рискованно, чем мелкой компании.) Очевидно, что класс риска заемщика влияет на рисковую структуру процентных ставок или относитель- [c.441]

Заметим, что третий фактор может быть интерпретирован как характеристика временной структуры процентных ставок, а четвертый фактор — как мера премии за риск неуплаты, которую инвестор требует за приобретение рисковых корпоративных облигаций вместо казначейских облигаций. [c.335]

Ожидаемый общий уровень инфляции, заложенный в затраты на капитал, выводится из временной структуры процентных ставок, которая формируется на основе доходности к погашению без рисковых правительственных облигаций, Номинальные процентные ставки правительственных облигаций воплощают реальную отдачу, требуемую инвесторами от своих вложений, плюс премия за ожидаемую инфляцию. Ожидаемую инфляцию можно определить как номинальную процентную ставку за вычетом оценочной реальной процентной ставки по следующей формуле [c.275]

На этапе количественного определения рисков проясняется взаимосвязь между структурой баланса и рисковыми позициями. Источниками информации при этом служат балансы рисков — риска недостачи, изменения процентных ставок, валютного риска и ликвидности. Эти балансы систематизируют активы и позиции банка в соответствии со связанными с ними рисками. С использованием балансов рисков проводят анализ чувствительности результата для построения моделей его зависимостей от конкретного фактора риска. Наибольшее затруднение при этом связано с локализацией влияния отдельных факторов риска. [c.213]

Влияние покупки ценных бумаг на открытом рынке на равновесную денежную массу. Покупка ценных бум.IT на открытом рынке приводит к снижению равновесной процентной ставки по федеральным фондам (см. рис. 25-10) с г° до г] (рис. А). До тех пор пока покупка ценных бумаг на открытом рынке явлжмся окончательной покупкой и обещает быть постоянной, ожидания размера процентной ставки по федеральным фондам также снизятся, а кривая доходности федеральных фондов сместится вниз (рис. Б). В дополнение, пока ФРС не влияет на рисковую структуру процентных ставок, кривая доходности казначейских ценных бумаг тоже должна сместиться вниз, а равновесная номинальная процентная ставка по 6-месячным казначейским ценным бумагам упадет с г° до г. Это, в свою очередь, приведет к увеличению равновесного спроса на деньги с М0 до А/, (рис. В). [c.692]

Выбор значения процентной ставки по федеральным фондам для достижения заданной денежной массы. Если промежуточной целью ФРС является денежная масса М, то номинальная процентная ставка, нужная для обеспечения спроса небанковского сектора на деньги, будет гп(М ), как показано на рис. Я При временной и рисковой структуре процентных ставок, описанных кривыми доходности (рис. 5), процентная ставка по федеральным фондам, согласующаяся с промежуточной целью денежно-кредитной политики, будет равна rt(M ). Следовательно, это и есть заданная процентная ставка по федеральным фондам, которую ФРС собирается таргетировать на рынке банковских резервов (рис. А). [c.695]

Другие эксперты ФРС должны будут установить взаимозависимость временной и рисковой структуры процентных ставок, таких, как кривые доходности, представленные на рис. 25-13 . Это поможет FOM определить размер процентной ставки по федеральным фондам, который он должен установить, чтобы достичь промежуточной цели денежно-кредитной политики. Эта заданная процентная ставка по федеральным фондам обозначена г.(А/ ) на рис. 25-13Б. [c.695]

Выбор целевой установки уровня заимствованных резервов для достижения промежуточной цели денежной кредитной политики. Если промежуточная цель ФРС — заданная денежная масса, равная М (рис. В), то, имея рисковую и временную структуры процентных ставок (рис. 6), ФРС необходимо таргетировать незаимствованные резервы, равные NBR (рис. А), чтобы достичь процентной ставки по федеральным фондам, согласующейся с промежуточной целью. Однако в случае изменения условий денежного рынка ФРС не изменяет заданную величину незаимствованных резервов, а позволяет процентным ставкам прийти в соответствие с ней. [c.699]

Структура процентных ставок

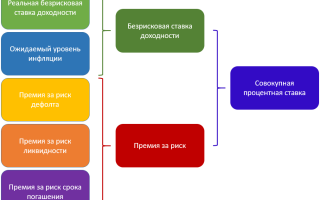
Пять составляющих процентной ставки

Структура процентной ставки или требуемой ставки доходности может быть декомпозирована на пять составляющих.

Реальная безрисковая ставка доходности

Ее величина не формируется под воздействием какого-либо риска или неопределенности, а отражает исключительно размер компенсации инвестору за отказ от текущего потребления. Другими словами, она представляет собой ставку безразличия, при которой для инвестора текущее потребление эквивалентно альтернативе вложения средств (без учета прочих факторов!).

Ожидаемый уровень инфляции

Этот компонент в структуре процентных ставок отражает ожидания рынка относительно роста агрегированных цен. Инфляция снижает покупательную возможность денег, то есть делает их стоимость в будущем ниже, чем в настоящий момент времени. Сумма реальной безрисковой ставки и ожидаемой инфляции является безрисковой ставкой доходности.

Премия за риск дефолта

Данная составляющая процентной ставки отражает риск дефолта у конкретного эмитента. Другими словами, всегда существует вероятность того, что заемщик может не соблюсти график платежей, либо вообще не сможет выполнить своих обязательства. Величина премии за риск дефолта зависит от кредитоспособности эмитента, одной из метрик которой является присвоенный кредитный рейтинг.

Премия за риск ликвидности

Само по себе понятие ликвидность означает способность ценной бумаги трансформироваться в денежные средства. При этом важнейшими факторами являются время, затраченное на такую трансформацию, и потеря стоимости в ее процессе. Если ценная бумага может быть продана в любой момент времени без потери стоимости, то она считается абсолютно ликвидной.

Рассмотрим данную ситуацию на примере. Допустим, что инвестор рассматривает возможность приобретения облигаций двух корпораций. При этом одну из них он может продать в любой момент времени с дисконтом в 30% к ее текущей рыночной стоимости, а вторую с дисконтом в 10%. Это означает, что вторая облигация более ликвидна по сравнению с первой. Таким образом, если все остальные параметры этих облигаций одинаковы, первая из них должна предлагать инвестору более высокую процентную ставку в качестве компенсации за принимаемый более высокий риск ликвидности.

Итак, чем ниже ликвидность ценной бумаги, тем выше премия за риск ликвидности в структуре процентной ставки, и наоборот.

Премия за риск срока погашения

При прочих равных условиях рыночная стоимость облигации с большим сроком погашения более уязвима к изменению процентных ставок. Из этого следует логическое заключение, что риски для инвестора растут вместе с увеличением срока погашения. Следовательно, размер премии за риск срока погашения у 20-ти летних облигаций будет выше, чем у 10-ти летних.

Схема

Схематически структура процентных ставок может быть представлена следующим образом.

Как можно видеть на схеме, сумма реальной безрисковой ставки доходности и ожидаемого уровня инфляции формируют безрисковую ставку доходности.

При этом совокупность премий за риск дефолта, ликвидности и срока погашения формируют премию за риск для конкретного эмитента.

В свою очередь, сумма безрисковой ставки доходности и премии за риск является требуемой ставкой доходности.

Виды и временная структура процентных ставок. Теории временной структуры процентных ставок

Временная структура процентных ставок – оценка динамики процентных ставок во времени, прогнозируемая с учетом ожидаемых темпов инфляции и объемов предложения и спроса на деньги.

1. Теория формирования реальной процентной ставки с учетом фактора инфляции. В основе расчета реальной процентной ставки с учетом фактора инфляции лежит Модель Фишера:

,

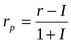r_p – реальная процентная ставка (фактическая или прогнозируемая в определенном периоде),

r – номинальная процентная ставка;

I – темп инфляции.

Пример, Необходимо рассчитать реальную годовую процентную ставку на предстоящий год.

r – номинальная годовая процентная ставка по опционным и фьючерсным операциям на фондовой бирже на предстоящий год сложилась в размере 19%;

I – прогнозируемый годовой темп инфляции= 7%.

Решение: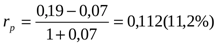

2. Теория оценки стоимости денежных средств с учетом фактора инфляции позволяет осуществлять расчеты как будущей, так и настоящей их стоимости с «инфляционной составляющей». В основе этих расчетов лежит формируемая реальная процентная ставка.

1) при оценке будущей стоимости денежных средств с учетом фактора инфляции:

FV_н – номинальная будущая стоимость вклада (денежных средств), учитывающая фактор инфляции;

Р – первоначальная сумма вклада (денежных средств);

r_p— реальная процентная ставка;

I – прогнозируемый темп инфляции

n – количество интервалов, по которым осуществляется каждый процентный платеж, в общем обусловленном периоде времени.

Пример: Определить номинальную будущую стоимость вклада с учетом фактора инфляции при следующих условиях:

n = 3 года – общий период размещения вклада.

Решение: S_н = 1000·[1+0,20)·(1+0,12)] 3 = 2428 долл.

2) При оценке настоящей стоимости денежных средств с учетом фактора инфляции:

PV_р =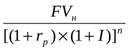

РV_р – реальная настоящая сумма вклада (денежных средств), учитывающая фактор инфляции;

FVн – ожидаемая номинальная будущая стоимость вклада (денежных средств).

Существует несколько теорий временной структуры процентных ставок, но все они являются разновидностями 3 осн.овныхнаправлений:

1.Теория предпочтения ликвидности

Теория предпочтения ликвидности – доходность долгосрочных активов в среднем должна превышать доходность аналогичных инструментов с меньшим сроком погашения, т.к. первые подвержены более высокому процентному риску. Поэтому инвесторы будут согласны заплатить некоторую премию за приобретение краткосрочных активов с целью избежания риска, связанного с долгосрочным инвестированием.

С другой стороны, заемщики предпочитают привлекать средства на долгосрочной основе и т.о. для привлечения средств на долгосрочной основе заемщики должны предложить инвестору дополнительную премию за риск ликвидности в виде более высокого дохода. В этом случае кривая доходности будет характеризоваться возрастанием доходности даже в отсутствии ожидания будущего повышения ставок.

Теория ожидания предполагает, что форвардная ставка пред. собой усредненное ожидание спот-ставки.

Спот-ставку обычно рассматривают как доходность к погашению бескупонной облигации и ее величину за t-период рассчитывается по формуле:

N – сумма, погашаемая через T периодов

P – текущая рыночная цена

Форвард ставкой м/д период t и t-1 является величина = 1+t-1ft=(1+rt)t/(1+rt-1)t-1

Теория сегментации основывается на представлении о существовании различных сегментов рынка. В соответствии с этой теорией считается, что инвесторы и заемщики по объективным и субъективным причинам привязаны к определенным видам ценных бумаг и срокам их обращения.

Согласно теории сегментации, возрастание кривой доходности наблюдается в том случае, если пересечению кривых спроса и предложения для краткосрочных инвестиций соответствует меньшая процентная ставка, чем для равновесных долгосрочных инвестиций.

Целью теории является создание моделей временной структуры процентной ставки.

1) статические модели, базирующиеся на классических методах прогнозирования временных рядов;

2) модели изменчивости, которые учитывают изменения дисперсий и ковариации;

3) стахостические – в основе лежит тот или иной случайный процесс.

Временная структура процентных ставок;

В настоящей главе рассматриваются кривая доходности процентных инструментов и теории временной структуры процентных ставок.

Вначале мы остановимся на определении кривой доходности, кривой доходности спот, выведем формулу для расчета теоретической ставки спот. После этого дадим определение форвардной процентной ставки и найдем формулу для ее вычисления. Далее представим три теории временной структуры процентных ставок, а именно, теории чистых ожиданий, предпочтения ликвидности и сегментации рынка.

В один и тот же момент на рынке обращаются облигации, до погашения которых остается различное время. Поэтому можно построить график зависимости доходности бумаг от срока, остающегося до погашения. Для этой цели используют облигации, с одинаковыми характеристиками, например, относящимися к одному классу риска. По оси ординат откладывается уровень процентной ставки, по оси абсцисс — время до погашения. Исходя из конъюнктуры рынка, кривая доходности, ее также именуют временной структурой процентных ставок, может иметь различную форму, как представлено на рис. 3-6.

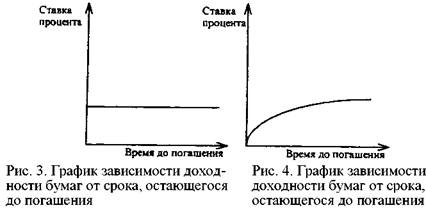
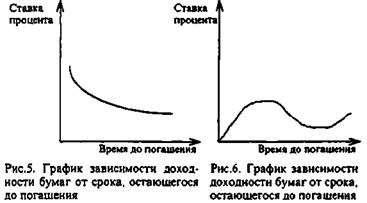
На рис. 3 кривая доходности параллельна оси абсцисс. Это означает, что процентная ставка одинакова для облигаций с различными сроками погашения. Рис. 4 показывает: процентная ставка возрастает по мере увеличения срока обращения облигаций. Данная форма кривой наиболее характерной для рынка. На рис. 5 представлена обратная ситуация. Рис. 6 описывает конъюнктуру, когда среднесрочные ставки по облигациям выше краткосрочных и долгосрочных. Построив кривую доходности, аналитик получает картину распределения процентных ставок во времени.

Для анализа ситуации на рынке большую роль играет кривая доходности, построенная на основе облигаций с нулевым купоном. Она представляет собой зависимость между доходностью и временем до погашения бескупонных облигаций. Аналитик использует ее для определения возможности совершения арбитражной операции. Любую купонную облигацию можно представить как совокупность облигаций с нулевым купоном, номинал которых равен купону и нарицательной стоимости облигации (для последнего платежа) и выпущенных на сроки, соответствующие срокам погашения купонов и облигации. Доходность купонной облигации и облигаций с нулевым купоном должна быть одинакова, в противном случае возникнет возможность совершить арбитражную операцию. Например, если доходность облигаций с нулевым купоном ниже, чем купонной облигации, то инвестор купит купонную облигацию и продаст пакет облигаций с нулевым купоном, платежи по которым будут соответствовать по размеру и времени платежам по купонной облигации. По данной операции вкладчик получит прибыль, поскольку пакет дисконтных облигаций стоит больше, чем купонная облигация. Если купонная облигация имеет более низкую доходность, чем соответствующая ей дисконтная облигация, то инвестор купит облигации с нулевым купоном таким образом и на такие суммы, чтобы их погашение соответствовало погашению купонов и номинала для купонных облигаций, и продаст созданную им искусственным образом купонную облигацию. Поскольку в этом случае купонная облигация стоит дороже приобретенного вкладчиком пакета облигаций с нулевым купоном, то он получит прибыль.

Различают спотовую процентную ставку и форвардную ставку. Спотовая ставка для периода в п лет — это ставка для облигации с нулевым купоном, до погашения которой остается п лет. Например, эмитируется дисконтная облигация на 1 год с доходностью 10%. Это означает, что ставка спот на один год равна 10%. Выпускается облигация на 2 года с доходностью 11%. Это означает, что спотовая процентная ставка на два года равна 11% и т. д. График зависимости между енотовыми ставками и временем до погашения облигации, называется кривой доходности спот.

Располагая данными о ставках спот за п периодов начисления процента и цене купонной облигации за период п + 1, можно рассчитать теоретическую ставку спот для периода п + 1.

Ставка спот на один год составляет 10%, на два — 11%; купонная облигация, до погашения которой остается три года, продается по цене 916 руб.; номинал облигации — 1000 руб.; купон 8% и выплачивается один раз в год. Необходимо определить теоретическую ставку спот для трех лет.

Как было отмечено выше, доходность купонной облигации и пакета дисконтных облигаций должны быть равны, чтобы исключить возможность арбитражных операций. Поэтому должно выполняться следующее равенство

где: r — теоретическая ставка спот для трех лет.

Решая уравнение, получаем, что r = 11, 5%. Аналогичным образом определяется теоретическая ставка спот для каждого следующего периода. Запишем использованное уравнение в общем виде:

купон облигации, до погашения которой осталось п периодов;

Р— цена купонной облигации;

N— номинал купонной облигации;

r1, r2. rn-1 — известные ставки спот для соответствующих периодов;

rn — ставка спот, величину которой требуется рассчитать.

Допустим, что в приведенном выше примере фактическая трехлетняя ставка спот на рынке равна 11%. Тогда инвестор может купить купонную облигацию за 916 руб. и выпустить три дисконтных облигации (или векселя) с номиналами 80 руб., 80 руб., и 1080 руб., и сроками погашения соответственно через один, два и три года. Пакет дисконтных облигаций стоит 927, 35 руб. Поэтому прибыль вкладчика с одной облигации равна:

927,35-916 =11,35 руб.

Если фактическая трехмесячная ставка спот составляет 13%, инвестор купит дисконтные облигации с номиналами 80 руб., 80 руб., и 1080 руб. и сроками погашения соответственно через один, два и три года за 886, 15 руб., эмитирует на ее основе купонную облигацию (или пакет процентных векселей) и продаст ее за 916 руб. Его доход составит:

916-886,15 = 29,85 руб.

Форвардная процентная ставка — это ставка для периода времени в будущем. Она определяется ставкой спот.

Ставка спот на один год составляет 10%, на два — 11%. Определить форвардную ставку для второго года, т. е. ставку спот, которая будет на рынке через год для облигации с нулевым купоном, выпущенной на год.

Допустим, вкладчик покупает облигацию с нулевым купоном, эмитированную на два года с номиналом 1000 руб. Тогда он платит за нее:

1000(1,11)2 = 811,62 руб.

Инвестор может выбрать иную стратегию, а именно, купить годичную облигацию и после ее погашения реинвестировать средства еще на год. Ему безразлично, какую стратегию выбрать, если во втором случае он также получит через два года 1000 руб., инвестировав сегодня 811, 62 руб. Чтобы ответить на вопрос, под какой процент ему следует реинвестировать средства на второй год, составим уравнение:

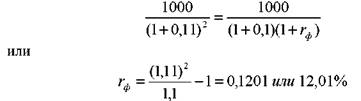
Запишем уравнение определения форвардной ставки в общей форме:

для периода п — (п — 1);

rп — ставка спот для периода п;

rn-1 — ставка спот для периода п — 1.

Между доходностью купонной облигации, бескупонной облигации и форвардной ставкой существуют соотношения, которые представлены на рис. 7 и рис. 8.