Критериальный анализ это

Большая Энциклопедия Нефти и Газа

Критериальный анализ

Правильно проведенный критериальный анализ сразу же позволяет наметить значение внешних параметров, при которых в первую очередь следует изучать процесс. Например, очевидно, что изучая процессы с разным Re, чтобы выявить все их особенности, надо брать интервалы с Re существенно большими и меньшими единицы и Re близкими к ней. [1]

Возможность использования критериального анализа при вероятностных исходных данных первоначально покажем на примере экономического обоснования надежности элементов системы электроснабжения. Основные трудности, которые возникают при оптимизации систем электроснабжения, заключаются в отсутствии достаточно объективной оценки ущербов народного хозяйства из-за перерывов в электроснабжении. Поэтому и целесообразно использовать критериальные зависимости, позволяющие производить анализ при неполных исходных данных. [2]

Таким образом, критериальный анализ можно использовать и-при наличии ограничений, накладываемых на оптимизируемые параметры, но при условии, что модифицированная функция Лагранжа имеет каноническую форму. [3]

Таким образом, приведенный критериальный анализ способствует разработке оптимальной конструкции различных деталей и узлов инжекционной части прямоточно-центробежных элементов. [4]

Если с помощью критериального анализа удается показать, что даже при очень больших изменениях входных параметров Xt решение остается нечувствительным, то можно считать задачу решенной. Такой путь весьма рационален. Часто при реализации полученного результата приходится считаться с жестко заданной стандартами шкалой параметров. Влияние та-кого отклонения при выборе ближайшего к результату допустимого по стандарту значения параметра также может быть надежно проконтролировано. [5]

Одна из характерных черт критериального анализа заключается в том, что в качестве базисных величин при технико-экономическом исследовании принимаются экономические значения параметров и затрат. [6]

Далее в разделе приведены результаты критериального анализа применения МУН на месторождениях с карбонатными коллекторами юга Пермской области. Из большого числа разрабатываемых, испытуемых и тиражируемых методов увеличения нефтеотдачи пластов выделяются следующие группы: 1) гидродинамические, 2) физико-химические, 3) микробиологические и 4) термические. В НИИнефтеотдача разработаны и апробированы в промысловых условиях технологии повышения нефтеотдачи, относящиеся к первым трем группам. Каждой из перечисленных групп соответствует своя область использования, регламентируемая исходными геолого-физическими и физико-химическими свойствами пластовой системы, обеспеченностью реагентами, технологическими и технико-экономическими показателями процессов. Например, термические методы целесообразно применять при значениях вязкости нефти более 100 — 150 мПа — с ввиду большого технологического эффекта от снижения вязкости при нагреве. [7]

Разработка конструкции выбранных механизмов и их критериальный анализ наиболее эффективно может проводиться с использованием дисплея. Разработка динамических моделей ведется с учетом заданных условий, которыми могут являться заданный тип привода, его автономность, конструктивные особенности передающих механизмов и др. В последующем динамические модели могут уточняться по результатам экспериментальных исследований и сопоставления их с результатами динамического синтеза. После разработки конструкции производится изготовление экспериментальных моделей, их экспериментальное исследование, а также определяются данные для динамического синтеза ( жесткост-ные характеристики, зазоры, коэффициенты трения и др.) и пределы изменения переменных параметров. При этом используются результаты экспериментальной проверки исследуемых механизмов. Динамический синтез ведется посредством аналоговых ЭВМ или устройств типа дисплея, что учитывается при разработке алгоритма синтеза. При динамическом синтезе используются данные экспериментов, а его результаты сопоставляются с ограничениями, принятыми при кинетостатическом синтезе и учитываются при окончательной отработке конструкции механизмов. [8]

Наиболее общий подход к решению оптимизационных задач методами критериального анализа с учетом технических ограничений и составляет сущность критериального программирования. [9]

В § 3 — 28 показана возможность применения критериального анализа для определения оптимальных вариантов при условии, что на оптимизируемые параметры накладываются функциональные ограничения типа неравенств. [10]

Рассмотрим несколько характерных задач, на которых проиллюстрируем возможность критериального анализа канонических уравнений . [11]

Руководитель или эксперт обладает необходимым опытом и знаниями, способен осуществить критериальный анализ ситуации , прогнозировать динамику событий, оценить важность используемых критериев, дать критериальную оценку значениям физических параметров и построить функцию предпочтения. [12]

Математическая модель ( 53) рассматривается в дальнейшем как основная для критериального анализа городских систем электроснабжения . [13]

АЭ-метод выступает как самостоятельный, если по его оценке, полученной на основании критериального анализа зарегистрированной АЭ-информации от источников-дефектов, состояние объекта признается удовлетворительным. В противном случае для окончательной оценки привлекаются дополнительные методы НК. Наибольшую надежность оценки дает применение АЭ-метода в комплексе с такими традиционными методами, как визуально-оптический, капиллярный, магнитопорошковый, ультразвуковой, рентгеновский. Эффективность комплексного контроля в этом случае определяется тем, что в задачу АЭ-метода входит выявление АЭ-активных источников и определение их координат или зон их расположения, обеспечивающих многократную минимизацию объемов последующего контроля традиционными методами. [14]

Критериальный анализ текста

В этой главе будут рассматриваться возможности качественного критериального анализа текста, чтобы в практической части разработать критерии анализа для задач данного исследования.

Обратимся к контент-анализу или анализу содержания. Это стандартная методика исследования в области общественных наук, предметом анализа которой является содержание текста.

Контент-аналитическое исследование личности базируется на свободно порожденном тексте, т. е. субъект при его создании выбирает наиболее подходящие слова для описания психоло­гического содержания. Однако при этом нет гарантии, что интересующие исследователя темы будут затронуты [2, с.29].

В разработке и практическом применении контент-анализа выделяют несколько стадий. После того, как сформулированы тема, задачи и гипотезы исследования, определяются категории анализа — наиболее общие, ключевые понятия, соответствующие исследовательским задачам. Система категорий играет роль вопросов в анкете и указывает, какие ответы должны быть найдены в тексте.

Категории контент-анализа должны быть исчерпывающими (охватывать все части содержания, определяемые задачами данного исследования), взаимоисключающими (одни и те же части не должны принадлежать различным категориям), надежными (должно быть однозначно ясно, какие части содержания следует относить к той или иной категории) и уместными (соответствовать поставленной задаче и исследуемому содержанию). При выборе категорий для контент-анализа следует избегать крайностей: выбора слишком многочисленных и дробных категорий, почти повторяющих текст, и выбора слишком крупных категорий, т.к. это может привести к упрощенному, поверхностному анализу. Иногда необходимо принимать во внимание и отсутствующие элементы текста, которые могут быть значимыми для контент-анализа.

После того, как категории сформулированы, необходимо выбрать соответствующую единицу анализа — лингвистическую единицу речи или элемент содержания, служащие в тексте индикатором интересующих исследователя явления. В практике отечественных контент-аналитических исследований наиболее, употребительными единицами анализа являются слово, простое предложение, суждение, тема, автор, герой, социальная ситуация, сообщение в целом и др. Сложные виды контент-анализа обычно оперируют не одной, а несколькими единицами анализа [14].

Если в качестве единицы анализа избирается тема, то она также выделяется в соответствии с некоторыми правилами:

§ Тема не может выходить за пределы абзаца.

§ Новая тема возникает, если происходит смена: воспринимающего, действующего, цели, категории.

Этапы работы с текстом при качественном анализе содержания [7]:

1. Предварительный этап: очищение текста, включающее выбрасывание безинформативных реплик, повторений, переформулировок, отвергнутых утверждений и т.п.. Уяснение текста, что требует представления текста в максимально определенной форме, но без изменения того значения, которое вкладывает респондент.

2. Разбиение текста на фрагменты, которые содержат отдельные высказывания или утверждения респондента, описывающие или интерпретирующие его мысли и чувства.

3. Объединение этих единиц в аналитические категории, которые относятся к одной и той же психологической идее.

4. Объединение этих аналитических категорий в более широкие и абстрактные принципы – понятия, которые выявляют структуру представлений автора о реальности (например, «Я-концепция»).

Таким образом, мы видим, что ключевым моментов в такого рода анализе текстов является формулирование категорий анализа таким образом, чтобы они отвечали задачам исследования с одной стороны, и были удобны, пригодны для того, чтобы выделять их в самом тексте. В экспериментальной части данного исследования будет предпринята попытка такие категории выделить и оформить.

Экспериментальная часть

Общая гипотеза исследования состоит в том, что в инициативных подростковых текстах проецируется мифологизированная идеальная форма данного возраста, подростковый герой.

Также выдвигаются следующие рабочие гипотезы:

· Основной сюжет подростковых инициативных текстов будет связан с темой признания – признания героя самим собой и окружающими людьми, поиск своего места в мире, самоопределение.

· Возрастная когорта не является гомогенной и в ходе исследования мы обнаружим расхождение паспортного и психологического возраста.

Объектом исследования являются авторы текстов, находящихся в подростковом возрасте.

Исследование состоит из следующих этапов:

1. Разработка анкеты на возрастные характеристики

2. Формулировка критериев, по которым можно будет идентифицировать проявления описания идеальной формы в подростковом тексте.

3. Разработка структуры анализа текстов

4. Инициирование подростков к написанию текстов. Был объявлен конкурс на подростковую сказку. Задание звучало следующим образом: «Всем известна поговорка «Сказка — ложь, да в ней намек. » и все знают, что в конце любой сказки есть какая-то мораль. Предлагаем вам написать сказку с такой моралью (намеком, уроком, жизненным правилом), которая была бы полезна для вас и ваших сверстников в сегодняшнем мире». Конкурсная форма выбрана исходя из предположения о том, что инициативный текст (порождаемый не по заданию, а по личному желанию человека этот текст написать) будет в большей степени проективен. Чтобы минимизировать риск того, что текст будет писаться ради приза, а не ради самого написания текста, призом конкурса была объявлена публикация этого текста в газете. Форма сказки была выбрана в связи с тем, что сама структура сказки аналогична описываемой Б.Д. Элькониным структуре событийности.

5. Анализ типажей героев и основных конфликтов подростковых тестов.

6. Категориальный анализ текстов.

7. Анализ полученного материала: применение U-критерия Манна-Уитни для обнаружения связи между выделенными в текстах категориями и возрастной характеристикой авторов текстов.

8. Оформление результатов исследования, подтверждение или опровержение гипотез.

КРИТЕРИАЛЬНЫЙ ЯЗЫК

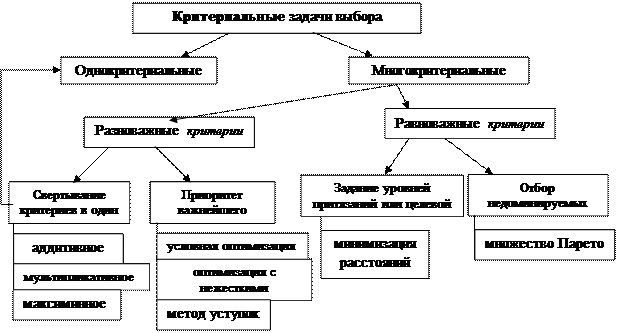
Рис. 7.4.1. Классификация задач выбора и способов их решения при их описании на критериальном языке

Выбор как максимизация критерия. Если сделать предположение, что выбор любой альтернативы приводит к однозначно известным последствиям (т.е. считать, что выбор осуществляет­ся в условиях определенности) и заданный критерий q(x) численно выражает оценку этих последствий, то наилучшей альтернативой х* является, естественно, та, которая обладает наибольшим значением критерия:

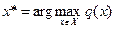(1)

Задача отыскания х*, простая по постанов­ке, часто оказывается сложной для решения, поскольку метод ее решения (да и сама возможность решения) определяется как характером множества X (размерностью вектора х и типом множества X — является ли оно ко­нечным, счетным или континуальным), так и характером критерия (является ли q(x) функ­цией или функционалом и какой или каким именно).

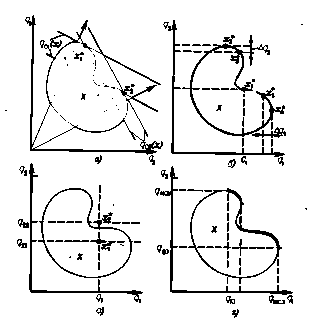
Иллюстрация методов решения многокритериальных задач: а) оптимизация по одному «суперкритерию», являющемуся линейной комбинацией частный критериев; б) метод усту­пок; в) задание уровней притязания; г) нахождение паретовского множества альтернатив

Однако сложность отыскания наилучшей альтернативы существенно возрастает, так как на практике оценивание любого варианта единственным числом обычно оказывается неприемлемым упрощением. Более полное рассмотрение альтернатив приводит к не­обходимости оценивать их не по одному, а по нескольким критериям, качественно различающимся между собой. На­пример, при выборе конструкции самолета проектировщикам следует учитывать множество критериев: технических (высотность, скорость, маневренность, грузоподъемность, длительность полета и т д.), техноло­гических (связанных с будущим процессом серийного изготовления са­молетов), экономических (определяющих затраты на производство, эксплуатацию и обслуживание машин, их конкурентоспособность), со­циальных (в частности, уровень шума, загрязнение атмосферы), эргоно­мических (условия работы экипажа, уровень комфорта пассажиров) и пр. Даже в обыденной жизни при выборе мы почти никогда не исполь­зуем единственный критерий: вспомните хотя бы затруднения при выбо­ре подарка ко дню рождения или при выборе места для стоянки в тур­походе.

Итак, пусть для оценивания альтернатив используется несколько критериев q_i (x), i=1. р. Теоретически можно представить себе слу­чай, когда во множестве X окажется одна альтернатива, обладающая наибольшими значениями всех р критериев; она и является наилучшей. Однако на практике такие случаи почти не встречаются, и возникает вопрос, как же тогда осуществлять выбор (так, например, на рис. 7.4.1.1. множеству X соответствуют внутренние точки фигуры на плоскости зна­чений двух критериев q_l и q₂; оба критерия желательно максимизиро­вать).

Способы решения много­критериальных задач. Первый способсостоит в том, чтобы многокрите­риальную задачу свести к однокритериальной. Это означает введение суперкритерия, т.е. скалярной функции векторного аргумента:

Суперкритерий позволяет упорядочить альтернативы по величине q, выделив тем самым наилучшую (в смысле этого критерия). Вид функ­ции q определяется тем, как мы представляем себе вклад каждого критерия в суперкритерий; обычно используют аддитивные или муль­типликативные функции:

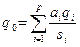(3)

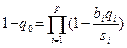(4)

Коэффициенты s_i обеспечивают, во-первых, безразмерность числа q_i/s_i (частные критерии могут иметь разную размерность, и тогда некоторые арифметические операции над ними, например сложение, не имеют смыс­ла) и, во-вторых, в необходимых случаях (как в формуле (4)) выпол­нение условия b_i q_i/s_i ≤1. Коэффициенты a_i и b_i отражают относительный вклад частных критериев в суперкритерий.

Итак, при данном способе задача сводится к максимизации супер­критерия:

х* = arg 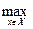q(q₁(x). q_p(x)) (5)

Очевидные достоинства объединения нескольких критериев в один суперкритерий сопровождаются рядом трудностей и недостатков, кото­рые необходимо учитывать при использовании этого метода. Оставив в стороне трудности построения самой функции и вычислительные трудности ее максимизации, обратим внимание на следующий очень важ­ный момент. Упорядочение точек в многомерном пространстве в прин­ципе не может быть однозначным и полностью определяется видом упо­рядочивающей функции.

Суперкритерий играет роль этой упорядочи­вающей функции, и его даже «небольшое» изменение может привести к тому, что оптимальная в новом смысле альтернатива окажется очень сильно отличающейся от старой. На рис. 7.4.1.1., а видно, как изменяется выбор наилучшей альтернативы при простой смене коэффициентов в линейной упорядочивающей функции (3) , что отражается в изменении наклона соответствующей прямой: q₀₁(x₁*) > q₀₁(x₂*), но q₀₂(x₁*)

Основные задачи критериального анализа;

В задачи критериального анализа входит широкий спектр проблем, связанных как с вопросами реализации технических средств моделирования, так и с вопросами обработки и интерпретации экспериментальной информации:

а) установление условий подобия;

б) установление условий распространения результатов единичного расчетно-аналитического или физического эксперимента, выполненного при данных параметрах, на другие объекты;

в) установление условий, при которых возможны обобщения экспериментальных и расчетных данных;

г) определение параметров модели.

Единичный эксперимент дает вполне определенный результат, который в ряде случаев удовлетворяет инженера при решении частной задачи. Однако при этом единичный эксперимент определяет поведение объекта именно в «единичных» условиях. В итоге кажущийся на первый взгляд достаточным результат фактически имеет небольшую практическую ценность.

Единичный результат не расширяет представлений исследователя не только с научной, но и с чисто практической точки зрения, так как отсутствует ответ на вопрос, что же будет происходить при изменениях параметров исследуемой системы или параметров ее режима.

Необходимо провести достаточный объем исследований, чтобы выявить влияние различных факторов и их изменений, которые могут происходить в различных сочетаниях, причем заранее неизвестно, как и в какой последовательности надо изменять эти факторы и какие их сочетания эквивалентны.

Исчерпывающий ответ на эти вопросы дает теория подобия в сочетании с теорией планирования эксперимента.

Возникает вопрос, нужно ли применение теории подобия и планирования эксперимента в таких часто встречающихся практических случаях, когда инженеру следует только проверить какой-либо образец, машину или установку на соответствие заданным техническим требованиям, то есть сказать «да — нет», «годится — не годится». Казалось бы, в этом случае теория подобия и теория планирования эксперимента не нужны.

Однако это далеко не так. История техники дает много примеров, когда именно решение частных, сугубо практических вопросов, приводило к катастрофическим последствиям. Например, мощные турбогенераторы, испытанные в полном соответствии с существующими нормативными требованиями, получали тяжелые повреждения в условиях ресинхронизации, когда сочетания ряда влия­ющих факторов оказывались отличными от нормативных.

В последние годы критериальный анализ всё чаще применяется для решения оптимизационных задач и, в частности, для исследования технико-экономиче­ских моделей систем электроснабжения и экономической устойчивости этих систем при отклонении их параметров от оптимальных значений.

Преимущества критериального анализа по сравнению с другими оптимизационными методами заключаются в том, что он придаёт исследованию обобщенный характер и позволяет решать ряд задач, не зная численного значения коэффициентов исследуемых уравнений.