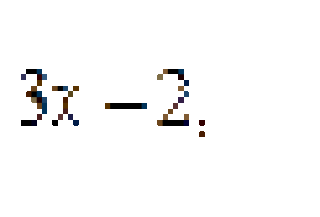Элементы матричного анализа

Элементы матричного анализа.

Тема 5.

Аудиторное изучение:

1. Векторы на плоскости и в пространстве..

2. Линейные операции над векторами, признаки коллинеарности векторов.

3. Разложение вектора по базису.

4. Координаты суммы векторов и произведения вектора на число.

5. Проекция вектора на ось, свойства.

Самостоятельное изучении:Векторы в пространстве. Построение векторов. Векторное решение задач.

Тема 6.

Аудиторное изучение

1. Скалярное произведение векторов его свойства. Выражение скалярного произведения через координаты перемножаемых векторов.

2. Векторное произведение векторов, его свойства. Выражение векторного произведения через координаты.

3. Смешанное произведение, свойства. Выражение смешанного произведения через координаты векторов.

Самостоятельное изучении:Геометрические приложения скалярного, векторного и смешанного произведения векторов. Решение задач.

Тема 7.

Аудиторное изучение

1. n-мерный вектор, n-мерное векторное пространство. Евклидово пространство.

2.Линейные операторы. Собственные векторы и собственные значения линейного оператора. Квадратичные формы.

Самостоятельное изучение:Декартова система координат на плоскости и в пространстве. Полярная система координат. Векторы на плоскости и в пространстве Аксиоматические построения и системы аксиом, n-мерный вектор и векторное пространство. Решение задач.

Тема 8.

Аудиторное изучение

1. Линейные операторы.

2. Собственные векторы и собственные значения линейного оператора.

3. Квадратичная форма. Приведение квадратичной формы к каноническому виду.

Самостоятельное изучение: Приведение квадратичной формы к каноническому виду. Линейные и аффинные преобразования плоскости.

ДЕ 3.

Аналитическая геометрия на плоскости

Тема 9.

Аудиторное изучение:

1. Линия на плоскости и ее уравнение.

2. Прямая на плоскости.

3. Уравнение прямой с угловым коэффициентом.

4. Уравнение прямой в отрезках.

5. Уравнение прямой, проходящей через две точки.

6. Общее уравнение прямой.

Самостоятельное изучение:Прямая в аффинном пространстве. Уравнения прямой в полярных координатах. Решение задач.

Тема 10.

Аудиторное изучение:

1. Угол между прямыми, условие параллельности, перпендикулярности прямых.

2. Нормальное уравнение прямой.

3. Расстояние от точки до прямой.

Самостоятельное изучение:Решение задач.

Тема 11

Аудиторное изучение:

3. Гипербола (определение, вывод канонического уравнения, оптическое свойство, касательная).

Самостоятельная работа: Геометрические свойства кривых второго порядка. Директрисы эллипса и гиперболы.

Тема 12.

Аудиторное изучение

1. Деление отрезка в данном отношении.

2. Преобразования прямоугольных координат.

3. Приведение линии второго порядка к каноническому виду.

Самостоятельное изучение: Прямая и плоскость в аффинном пространстве. Приведение уравнений второго порядка к каноническому виду. Построение кривых второго порядка.

ДЕ 4

Тема 13.

Аудиторное изучение

1. Плоскость в пространстве.

2. Различные виды уравнений плоскости.

3. Угол между плоскостями, условие параллельности и перпендикулярности плоскостей.

4. Формула расстояния от точи до плоскости.

Самостоятельное изучение: Векторное и параметрические уравнения плоскости. Замена системы координат.

Тема 14.

Аудиторное изучение

1. Прямые в пространстве (канонические и параметрические уравнения).

2. Уравнения общего перпендикуляра к скрещивающимся прямым, расстояние между скрещивающимися прямыми.

Самостоятельное изучение: Векторное уравнение прямой в пространстве. Уравнения проекций прямых на оси координат. Решение задач.

Тема 15.

Аудиторное изучение

1. Поверхности в пространстве.

2. Поверхности второго порядка.

Самостоятельное изучение: Поверхности второго порядка (эллипсоид, однополостной и двуполостной гиперболоид. Свойства поверхностей второго порядка. Уравнения множеств в пространстве.

Тема 16.

Аудиторное изучение

1. Приведение общего уравнения поверхности второго порядка к каноническому виду.

Самостоятельное изучение: Приведение общего уравнения линии второго порядка к каноническому виду. Решение задач.

Содержание лабораторных (или практических) занятий

ДЕ. 1.

Занятие 1. Матрицы, действия над ними.

План:

1. Основные понятия: Матрица, виды матриц.

2. Действия над матрицами и их свойства.

3. Решение задач.

Найти значение матричного многочлена f(A)

1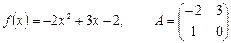

Ответ:

2.

Ответ:

3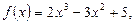

Занятие 2. Определители.

План:

1.Определители первого, второго, третьего порядков.

2. Свойства определителей.

3. Определители четвертого порядка.

4. Обратная матрица. Алгоритм нахождения обратной матрицы.

Раздел 3. Элементы матричного анализа. Векторы

Вопросы для подготовки к коллоквиуму

1. n-мерный вектор. Определение, линейные преобразования.

2. n-мерное векторное пространство. Определение, линейные (не)зависимые вектора.

3. Размерность векторного пространства. Базис. Координаты вектора в базисе.

4. Евклидово пространство. Определение, свойства, длина вектора.

5. Скалярное произведение.

6. Векторное произведение.

7. Смешанное произведение векторов.

8. Двойное векторное произведение.

9. Линейные операторы. Определение, свойства, действия над линейными операторами.

10. Собственные векторы и собственные значения линейного оператора.

Задания для аудиторной самостоятельной работы

1. На плоскости относительно некоторого базиса даны координаты трех векторов: ;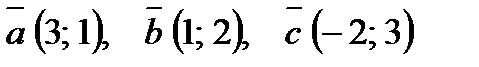

1) Найти координаты векторов ; .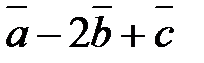

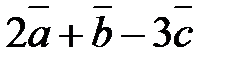2) Проверить, что векторы 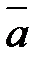и 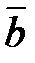образуют базис на плоскости. Найти координаты вектора 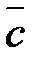в этом базисе.

3) Определить при каком значении параметра 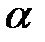векторы 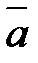и 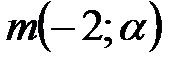будут коллинеарными.

4) Найти координаты вектора .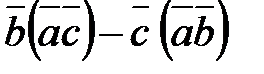

5) Вычислить , .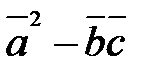

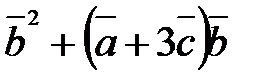6) Найти косинус угла между векторам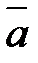и и .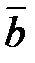

2. В пространстве относительно некоторого базиса даны координаты трех векторов: .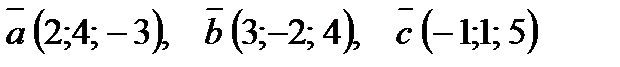

1) Найти координаты векторов , .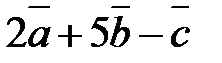

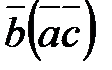2) Вычислить ; .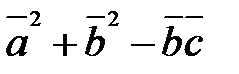

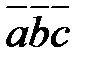3) Найти косинус угла между векторам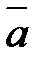и и .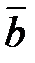

3. На плоскости относительно декартовой системы координат даны координаты трех точек: ;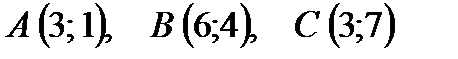

1. Координаты вектора .

2. Координаты точек 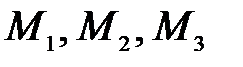, делящих отрезки 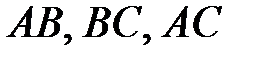в отношениях 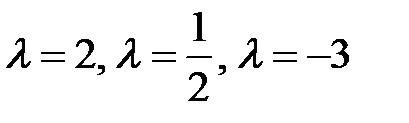, соответственно.

1. Площадь треугольника .
2. Угол .

Индивидуальное домашнее задание

Задание № 1. Даны векторы а=αm+βn и b=γm+δn, где |m|=k, |n|=l, (m,^n)=φ.

Найти: 1) (λ а+μ b)*(ν а+τ b); 2). пр_b(ν а+τ b); 3). Cos(a,^ τ b).

Элементы матричного анализа.

Векторы на плоскости и в пространстве. n-мерный вектор и векторное пространство. Размерность и базис векторного пространства. Переход к новому базису. Евклидово пространство. Линейные операторы. Собственные векторы и собственные значения линейного оператора. Квадратичные формы.

Вопросы для самоконтроля

1. Определение вектора на плоскости и в пространстве.
2. Координаты вектора.
3. Дать определение коллинеарных и равных векторов.
4. Линейные операции над векторами: сложение и вычитание двух векторов, умножение вектора на скаляр.
5. Скалярное произведение двух векторов.
6. Угол между векторами. Условие коллинеарности и перпендикулярности двух векторов.
7. Дать определение n-мерного вектора. Линейные операции над n-мерными векторами.
8. Дать определение векторного пространства.
9. Дать определение линейно независимых векторов.
10. Дать определение n-мерного векторного пространства.
11. Дать определение базиса n-мерного векторного пространства.
12. Теорема о представлении вектора через базис.
13. Переход к новому базису.
14. Дать определение линейного оператора.
15. Действия над линейными операторами.

16. Дать определение собственного вектора и собственного значения линейного оператора.

4. Элементы аналитической геометрии

Системы координат на прямой, плоскости и в пространстве. Основные задачи на метод координат (расстояние между двумя точками, деление отрезка в данном отношении).

Уравнение линии на плоскости. Уравнение прямой. Условие параллельности и перпендикулярности двух прямых. системы линейных неравенств.

Уравнение прямой и плоскости в пространстве.

Вопросы для самоконтроля

1. Дать определение системы координат на прямой, плоскости и в пространстве.
2. Записать формулу расстояния между двумя точками.
3. Записать формулы для нахождения координат середины отрезка.
4. Дать определение уравнения линии на плоскости.

5. Записать различные виды уравнения прямой на плоскости: уравнение с угловым коэффициентом; уравнение прямой, проходящей через две точки; уравнение прямой, проходящей через данную точку в данном направлении; уравнение прямой в отрезках; общее уравнение прямой. Пояснить смысл коэффициентов.

5. Основы оптимального программирования

Линейные задачи оптимизации. Основные определения и задачи линейного программирования. Симплексный метод решения задач линейного программирования. Целочисленное программирование.

Вопросы для самоконтроля

1. Общая постановка задачи линейного программирования (ЛП).
2. Дать определение допустимого решения задачи ЛП и области допустимых решений (ОДР).
3. Виды математических моделей.
4. Алгоритм графического метода решения задач ЛП.
5. Алгоритм симплексного метода.

6. Общая формулировка задачи целочисленного программирования.

Матричный анализ

Сумма элементов матрицы по строкам. Алгоритм нахождения обратной квадратной матрицы и ее определителя. Решение системы линейных уравнений методом Крамера и Гаусса. Построение математической модели экономического процесса и определение плана производства.

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФГБОУ ВПО Уральский государственный экономический университет

по дисциплине «Линейная алгебра»

Вычислить сумму матриц kA+mB, если

Элементы матрицы суммы определяются по формуле:

Вычислим элементы первой строки матрицы суммы:

Таким образом, матрица суммы примет вид:

Вычислить обратную матрицу и сделать проверку.

Используем алгоритм нахождения обратной матрицы:

1.Матрица квадратная (число строк равно числу столбцов), следовательно, обратная к ней матрица существует.

2.Находим определитель исходной матрицы:

3. Находим матрицу, состоящую из алгебраических дополнений элементов исходной матрицы:

Таким образом, получаем матрицу:

4.Полученную матрицу транспонируем:

5.Последнюю матрицу делим на определитель исходной матрицы и получаемобратную матрицу:

6.Осуществляем проверку полученного результата. Для этого находим произведение полученной матрицы на исходную:

Таким образом, получили в результате единичную матрицу. Следовательно, обратная матрица была найдена, верно.

Решить систему линейных уравнений методом Крамера, Гаусса.

1)Решить систему методом Крамера.

Составляем матрицу системы:

Вычисляем определитель этой матрицы:

Находим определители ?1, ?2, ?3, получающиеся из исходного определителя заменой соответственно первого, второго и третьего столбцов столбцомсвободных членов:

Теперь используя формулы Крамера

находим решение системы:

2) Решим систему методом Гаусса.

Составляем расширенную матрицу системы, в которую входят коэффициенты при переменных и свободные члены:

Умножим 2-ую строку на (5). Умножим 3-юу строку на (7). Добавим 3-ую строку к 2-ой:

Умножим 1-ую строку на (26). Умножим 2-ую строку на (3). Добавим 2-ую строку к 1-ой:

Из 1-ой строки выражаем x₃

Из 2-ой строки выражаем x₂

Из 3-ой строки выражаем x₁

матрица определитель линейный крамер гаусс

Вычислить определитель 4-го порядка

Запишем разложение определителя по четвертой строке:

где Aij — алгебраическое дополнение элемента ij a .

Найдем алгебраические дополнения по формуле А_ij=(-1) i + j , где m_ij— минор элемента ij a, который получается из исходного определителя вычеркиванием строки и столбца, на пересечении которых стоит данный элемент.

Подставляем полученные значения в разложение определителя:

матрица обратный определитель линейный крамер гаусс

Самостоятельно, по аналогии с примером, составить задачу с экономическим содержанием, построить математическую модель экономического процесса, и решить поставленную задачу.

Затраты трех видов сырья А, B, C на производство единицы каждого из трех типов продукции I, II, III и запасы каждого вида сырья заданы в таблице (Таблица 1):

Требуется определить план производства, обеспечивающий использование всего сырья.

Запишем систему линейных уравнений, используя данные, приведенные в таблице:

где — объемы выпускаемой продукции каждого вида.

Для решения воспользуемся методом Гаусса. Запишем расширенную матрицу системы:

Запишем систему в виде расширенной матрицы:

Умножим 2-ую строку на (-2). Добавим 2-ую строку к 1-ой:

Умножим 2-ую строку на (3). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:

Умножим 1-ую строку на (2). Добавим 2-ую строку к 1-ой:

Теперь исходную систему можно записать как:

Из 1-ой строки выражаем x₃

Из 2-ой строки выражаем x₂

Из 3-ой строки выражаем x₁

Размещено на allbest.ru

Подобные документы

Метод Гаусса — последовательное исключение переменных из системы уравнений. Определение понятия расширенной матрицы. Метод Крамера, расчет определителя системы. Метод обратной матрицы. Расчет алгебраических дополнений для элементов полученной матрицы.

презентация [184,4 K], добавлен 21.09.2013

Понятие обратной матрицы. Пошаговое определение обратной матрицы: проверка существования квадратной и обратной матрицы, расчет определителя и алгебраического дополнения, получение единичной матрицы. Пример расчета обратной матрицы согласно алгоритма.

презентация [54,8 K], добавлен 21.09.2013

Вычисление и построение матрицы алгебраических дополнений. Решение системы линейных уравнений по формулам Крамера, с помощью обратной матрицы и методом Гаусса. Определение главной и проверка обратной матрицы. Аналитическая геометрия на плоскости.

контрольная работа [126,9 K], добавлен 20.04.2016

Разложение определителя 4-го порядка. Проверка с помощью функции МОПРЕД() в программе Microsoft Excel. Нахождение обратной матрицы. Решение системы линейных уравнений методом обратной матрицы и методом Гаусса. Составление общего уравнения плоскости.

контрольная работа [138,7 K], добавлен 05.07.2015

Решение системы линейных уравнений по правилу Крамера и с помощью обратной матрицы. Нахождение ранга матрицы. Вычисление определителя с помощью теоремы Лапласа. Исследование на совместимость системы уравнений, нахождение общего решения методом Гауса.

контрольная работа [97,3 K], добавлен 24.05.2009

Правила произведения матрицы и вектора, нахождения обратной матрицы и ее определителя. Элементарные преобразования матрицы: умножение на число, прибавление, перестановка и удаление строк, транспонирование. Решение системы уравнений методом Гаусса.

контрольная работа [462,6 K], добавлен 12.11.2010

Выполнение действий над матрицами. Определение обратной матрицы. Решение матричных уравнений и системы уравнений матричным способом, используя алгебраические дополнения. Исследование и решение системы линейных уравнений методом Крамера и Гаусса.

контрольная работа [63,2 K], добавлен 24.10.2010

Расчет показателей матрицы, ее определителя по строке и столбцу. Решение системы уравнений методом Гаусса, по формулам Крамера, с помощью обратной матрицы. Вычисление предела без использования правила Лопиталя. Частные производные второго порядка функции.

контрольная работа [95,0 K], добавлен 23.02.2012

Линейные операции над матрицами. Умножение и вычисление произведения матриц. Приведение матрицы к ступенчатому виду и вычисление ранга матрицы. Вычисление обратной матрицы и определителя матрицы, а также решение систем линейных уравнений методом Гаусса.

учебное пособие [658,4 K], добавлен 26.01.2009

Решение системы уравнений по формулам Крамера, методом обратной матрицы и методом Гаусса. Преобразование и поиск общего определителя. Преобразование системы уравнений в матрицу и приведение к ступенчатому виду. Алгебраическое дополнение элемента.

контрольная работа [84,5 K], добавлен 15.01.2014
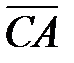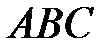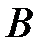