Детерминированный факторный анализ индексный метод
Индексный метод факторного анализа;
Сущность индексного метода факторного анализа состоит в следующем: во-первых, определяются индекс результативного показателя и индексы факторов; во-вторых, устанавливается схема взаимосвязи индекса результативного показателя с индексами факторов; в-третьих, составляется алгоритм расчетов влияния факторов на изменение результативного показателя.
Рассмотрим применение индексного метода факторного анализа на примере. Имеем информацию о выручке от продаж в торговой точке за два аналогичных периода времени.
B =10 тыс. шт. х 6 руб. = 60 тыс. руб.
В1 = 12 тыс. шт. х 9 руб. = 108 тыс. руб.
ΔВ = В1 — Во = 108 — 60 = +48 тыс. руб.
Рассчитаем индексы результативного показателя и индексы факторов:

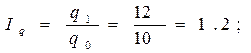
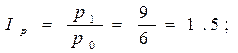
Взаимосвязь индекса результативного показателя с индексами факторов аналогична взаимосвязи самого результативного показателя с факторами, т.е.
Алгоритм I расчетов влияния факторов индексным методом
1) влияние на выручку изменения количества проданного товара
3) влияние на выручку изменения цены единицы товара
Проверка: ΔВ = В1 — Во = ΔВ (q) + ΔВ(р).
Расчеты влияния факторов:
1) ΔВ (q) = (1,2- 1,0) х 60 тыс. руб. = +12 тыс. руб.;
2) ΔВ (р) = (1,2 х 1,5- 1,2) х 60 тыс. руб. = +36 тыс. руб.
Проверка: ΔВ = 108 — 60 = 12 + 36, или
48 тыс. руб. = 48 тыс. руб.
Достоинство индексного метода состоит в том, что изменение результативного показателя раскладывается по факторам без остатка. Вместе с тем этому методу свойственен серьезный недостаток — элемент субъективизма. Он заключается в произвольном определении порядка расположения факторов в цепочке сомножителей.
Рассмотренный выше алгоритм соответствует только одному варианту расположения факторов, т.е.
С позиций математики равноправным является и другой вариант расположения факторов, т.е.
Однако второму варианту расположения факторов соответствуют другой алгоритм и другие результаты расчетов.
Алгоритм, 2 расчетов влияния факторов индексным методом
1) влияние на выручку изменения цены единицы товара
2) влияние на выручку изменения количества проданного товара
Проверка: ΔВ = В1 — Во = ΔВ (р) + ΔВ (q).
Расчеты влияния факторов:
1) ΔВ (р) = (1,5 — 1,0) х 60 тыс. руб. = +30 тыс. руб.;
2) ΔВ (q) = (1,5 х 1,2 — 1,5) х 60 тыс. руб. = +18 тыс. руб.
Проверка: ДВ = 108 — 60 = 30 + 18, или 48 тыс. руб. = 48 тыс. руб.
Таким образом, результаты расчетов влияния факторов по двум вариантам не совпадают. Причиной несовпадения является «неразложенный остаток». В первом варианте он «присоединился» к фактору «изменение цены единицы товара». Во втором — к фактору «изменение количества проданного товара».
С увеличением числа факторов-сомножителей резко возрастает количество равноправных вариантов расчетов, так как увеличивается число возможных перестановок факторов. Например, число перестановок из трех по три равно шести, из четырех по четыре — 24, а из пяти по пять — 120.
Для обоснования правильности только одного из многих вариантов экономисты вывели следующее правило индексного метода факторного анализа. Все факторы можно разделить на две группы:
1)количественные (первичные, или экстенсивные);
2)качественные (вторичные, или интенсивные).
При расстановке факторов в модели исходят из следующего: на первое место ставится количественный фактор, на второе — качественный. В соответствии с этим положением следует признать правильным первый из рассмотренных нами алгоритмов. Вместе с тем необходимо помнить, что данное правило субъективно.
Для лучшего понимания сущности индексного метода приведем алгоритм расчетов для решения трехфакторной мультипликативной модели.
расчетов влияния факторов индексным методом для решения трехфакторной мультипликативной модели
Способы детерминированного факторного анализа
Детерминированный факторный анализ — это методика изучения влияния факторов на результативный показатель, связь между которыми имеет функциональный характер. То есть результативный показатель представлен в виде произведения, алгебраической суммы или частного факторов.
Этапы проведения детерминированного факторного анализа:
· построение обоснованной детерминированной факторной модели;
· выбор приема факторного анализа;
· реализация расчетных процедур;
· формулирование выводов и рекомендаций по результатам анализа.
Построение факторной модели. В детерминированной факторной модели связи между переменными жестко фиксированы и каждой конкретной величине изменения независимой переменной (фактора) соответствует строго определенное (детерминированное) изменение зависимой переменной (результативного показателя).
На этом этапе происходит моделирование взаимосвязей между результативными показателями и факторами, которые влияют на их величину. Это очень важный этап, так как если на этом этапе будет допущена ошибка, то все дальнейшие расчеты не дадут верных результатов. Смысл этапа состоит в том, чтобы в форме математического уравнения выразить взаимосвязь исследуемого показателя и факторов.
Существует правило, которое заключается в следующем: любое расширение детерминированной факторной модели не должно противоречить логике связи «причина — следствие». То есть факторы, которые входят в модель, должны находиться в причинно-следственной связи с показателем. Кроме того, все показатели факторной модели должны быть количественно измеряемыми.
В зависимости от числа факторов, используемых в модели, модель может быть двух-, трех-, четырехфакторной и т. д.
Выделяют следующие виды детерминированных факторных моделей:
— аддитивная модель. Это модель, в которую факторы входят в виде алгебраической суммы
 ; (2)
; (2)
— мультипликативная модель. Это модель, в которую факторы входят в виде произведения
 ; (3)
; (3)
— кратная модель. Это модель, представляющая собой отношение факторов, то есть результативный показатель получают делением одного фактора на величину другого
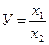 ; (4)
; (4)
— смешанная модель. Это модели, которые сочетают в себе различные комбинации предыдущих моделей
 ; (5)
; (5)
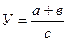 ; (6)
; (6)
 ; (7)
; (7)
Следующим этапом проведения детерминированного факторного анализа является выбор приема факторного анализа. Существует несколько способов проведения детерминированного факторного анализа:
1. Способ цепных подстановок.Способ цепных подстановок позволяет измерить влияние каждого отдельного фактора на прирост результативного показателя. Суть способа цепных подстановок заключается в последовательной замене базисной величины каждого фактора отчетными значениями и в оценке влияния произведенной замены на результативный показатель. К достоинству этого метода относится достаточная простота и универсальность. Способ цепных подстановок можно использовать для всех видов детерминированных факторных моделей (аддитивных, мультипликативных, кратных, комбинированных).
При использовании этого способа большое значение имеет очередность расстановки факторов в факторной модели и, соответственно, последовательность изменения значений факторов, так как от этого зависит количественная оценка влияния каждого фактора.
Для метода цепных подстановок должна применяться правильно построенная детерминированная факторная модель, должна соблюдаться определенная очередность в расстановке факторов. Если в факторной модели присутствуют количественные и качественные факторы, то замену факторов следует начинать с количественного фактора.
Количественные факторы отражают количественную определенность явлений. Количественные факторы могут выражаться как в стоимостном, так и в натуральном измерителях. Например, количественные факторы характеризуют объем производства и реализации продукции, причем величина этих факторов может быть выражена как в рублях, так и в штуках, метрах и т. д.
Качественные факторы характеризуют внутренние свойства, особенности и признаки изучаемых объектов. Например, качественным фактором является жирность молока, производительность труда, качество продукции и т. д.
Алгоритм расчета способом цепной подстановки для двухфакторной мультипликативной модели выглядит следующим образом:
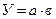 , (8)
, (8)
где а – количественный фактор;
в – качественный фактор.
Анализ начинают с того, что рассчитывают:
 (9)
(9)
 (10)
(10)
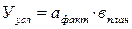 (11)
(11)
Далее определяют общее изменение результата (У):
 (12)
(12)
Определяют влияние факторов:
— количественного фактора по формуле
 (13)
(13)
— качественного фактора по формуле
 (14)
(14)
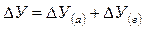 (15)
(15)
Рассмотрим алгоритм расчета на конкретном примере.
Пример 1.По исходным данным таблицы 1 определите отклонение объема производства в целом и за счет влияния факторов.
Таблица 1 – Исходные данные для факторного анализа
Методы детерминированного факторного анализа
Понятие детерминированного факторного анализа
Детерминированный факторный анализ – это метод исследования воздействия на объект факторов, которые связаны с результатом воздействия функционально.
То есть, детерминированный факторный анализ позволяет установить связь между итоговым показателем или функцией, а также факторами или аргументами функции. Для того, чтобы исследовать подобные зависимости необходимо соблюдать ряд требований, к которым относят:
- Рассматриваемые факторы должны относиться к реальной действительности, а не быть абстрактными. Они должны быть причиной или следствием рассматриваемого явления или объекта. Такие модели имеют высокий практический потенциал, в отличие от математических абстракций.
- Показатели рассматриваемой модели должны быть измеряемы количественно. Так же они должны иметь информационное описание.
- Рассматриваемые факторы могут быть оценены по отдельности. То есть, при исследовании взаимосвязи факторов с конечным результатом должна быть возможность увидеть их обособленное влияние на функцию. При этом их совокупное воздействие показывает прирост итогового результата.
Попробуй обратиться за помощью к преподавателям
Детерминированный анализ использует следующие виды моделей. Аддитивные модели используются в случае, если результат представляет собой совокупность нескольких факторных показателей. Математически эта зависимость отображается следующим уравнением:
$Y = x_1 + x_2 + x_3 + … x_n$
В случае, если результат воздействия факторов представляет собой их произведение, то пользуются мультипликативной моделью, которая выглядит как:
$Y = x_1 • x_2 • x_3 • … • x_n$
Если при вычислении необходимо разделить один фактор на другой, то пользуются кратными моделями, представленными такими уравнениями как:
Так же могут использоваться смешанные или комбинированные модели. Они строятся на сочетании разных комбинаций вышеперечисленных моделей. Для проведения операций с вышеперечисленными моделями могут использоваться следующие приемы. Например, прием удлинения, когда числитель формулы раскладывают на отдельные факторы. Еще один способ – способ формального разложения. В этом случае знаменатель раскладывается на составляющие факторы. Математическое уравнение:
Задай вопрос специалистам и получи
ответ уже через 15 минут!
$Y = Z / X = Z / x_1 + x_2+… + x_n$
Так же применяется способ расширения, который предполагает умножение числителя и знаменателя на одну или ту же величину, что позволяет исследовать влияние фактора на функцию в целом. Метод сокращения, напротив, позволяет разделить величины на указанный фактор.
Детерминированный факторный анализ предполагает применение различных методов манипулирования действующими факторами. Как правило, он позволяет методом исключения оставлять один фактор и исследовать его влияние на функцию. Для этого специалисты могут использовать методы цепной подстановки, абсолютные и относительные разницы, индексный метод, метод долевого участия и другое.
Метод цепной подстановки
Способ цепной подстановки факторов является наиболее универсальным. Он позволяет опытным и расчетным путем оценить влияние фактора на хозяйственный результат. Сущность метода заключается в замене базисной величины фактора на фактическую. Далее осуществляется вычитание из каждой замены предыдущего значения. На примере аддитивной модели метод цепной подстановки примет вид:
- Аддитивная модель $ Y = a + b + c$. Базисный фактор $a_0$ будет последовательно заменяться на каждый фактическое значение фактора $a_1$. При этом количество замен будет равняться количеству воздействующих факторов, то есть $Y_1 = a_1 + b_1 + c_1$
- Далее из полученного значения вычитается предшествующее. Каждый фактор будет рассматриваться в двух периодах – базисном и фактическом. Баланс отклонений дельты Y составит совокупность отклонений факторов $a, b, c$.
- Полученный результат $Y_0$ и $Y_1$ покажут изменение результата под воздействием факторов в аддитивной модели, где дельта $a, b, c$ – покажет дельту изменения итога.
Метод подстановок рассчитан на оценку количественных показателей. Только рассчитав их, исследователь может обратиться к качественным показателям. Расчет значений факторов позволяет определить как каждый из них влияет на конечный результат. Однако, использование этого метода требует знаний о последовательности влияния факторов на конечный результат. Так же необходимо учитывать их взаимное подчинение, чтобы иметь возможность их систематизировать.
Метод цепных подстановок является инструментом определения влияния структурного фактора на итог. Примером может послужить расчет выручки, который зависит не только от цены реализации, но и от количества проданных товаров, их структуры. То есть, продажа товаров более высокого качества принесет большую сумму дохода, нежели от товаров более низкого качества.
Метод абсолютных разниц
Этот способ применяется для моделей, где рассматривается произведение влияния фактора на конечный результат хозяйственной деятельности. То есть, он используется для моделей аддитивного и мультпликативно-аддитивного вида. Несмотря на то, что область его применения ограничена, он активно применяется в анализе экономической работы субъектов. Оценка проводится путем умножения абсолютного значения прироста на плановое расчетное значение. Таким образом, появляется возможность рассмотреть влияние одного фактора. Значение всех остальных факторов принимается как фактическое и неизменяемое, а последующих факторов в виде базиса.
Расчет воздействия начинается с первого фактора, далее строго соблюдается последовательность влияния факторов. Рассмотрим на примере мультипликативной модели:
- $Y (a) = a • b_0 • c_0$, фактор $а$ рассматривается в динамике его изменения, остальные факторы исследуются в их базисном значении.
- $Y(b) = a_1 • b • c_0$, то есть рассматриваемый фактор $b$ берется в динамике, предыдущий фактор a оценивается по его фактическому значению, а последующий фактор c по базисному.
- $Y (c) = a_1 • b_1 • c$, здесь соблюдается тот же принцип, что и вышеуказанных моделях.
Индексный метод оценки влияния факторов оперирует относительными величинами. Он помогает получить более точное представление о воздействии факторов, так как каждый фактор в его фактическом значении делится на его базисное значение, что позволяет рассчитать индекс. С помощью индексов можно охарактеризовать исследуемое явление во времени и пространстве.
Наиболее часто в экономике используют три вида индексов, а именно, индекс Ласпейреса или индекс фактического товарооборота. Агрегатный индекс цен или индекс Паше широко применяется для оценки динамики цен и зависимости производственного выпуска. Индексы позволяют анализировать влияние факторов в том случае, если оно представлено их произведением.
Интегральный метод является наиболее точным из существующих. Он полностью убирает эффект преувеличения влияния одного фактора, и преуменьшения влияния другого. Это происходит из-за того, что факторы оказывают взаимное влияние, а значит, образуют совместный прирост итогового значения.
Все рассмотренные методы факторного анализа работают для оценки количественного влияния факторов. При этом, исследование сложных факторов подразумевает, что они будут разбиты на более простые составляющие, а затем, элементы будут проанализированы по отдельности. В этом случае, разделенные факторы будут относится ко второму уровню, который рассчитывается с помощью метода долевого участия.
Этот способ представляет собой разбивку факторов на несколько уровней. Чтобы рассчитать факторы второго порядка проводится оценка динамики их прироста. Причем анализируется их доля в общей сумме прироста. Затем осуществляется их умножение на величину влияния совокупного раскладываемого фактора.
Применение методов детерминированного факторного анализа требует соблюдения условий, позволяющих избегать элиминирования. Оно предполагает, что изменение факторов происходит не зависимо друг от друга, когда в реальности все факторы, как правило, оказывают взаимное влияние. Прирост изменения итога обычно происходит по показателю, анализируемому в последнюю очередь. При исследовании модели очень важно учитывать эту особенность, так как месторасположения фактора в цепочке воздействия может влиять на общий результат и влияние других факторов. Помимо приведенных методов, все чаще используются интегральный метод, метод логарифмический, кольцевой, экстремальный и метод взвешенных конечных разностей.
Таким образом, детерминированный факторный анализ и его методы позволяют оценивать влияние факторов на конечный результат. Он широко применяется при анализе хозяйственной деятельности отдельных субъектов хозяйствования и целых систем. Важно помнить, что ни одна структура не является закрытой, а значит, всегда подвержена воздействию других систем, событий, явлений и объектов. При этом сам предмет исследования может оказывать влияние на окружающую среду. Кроме того, детерминированный факторный анализ помогает рассматривать экономические показатели в динамике, что позволяет приблизить исследование к реальности.
Так и не нашли ответ
на свой вопрос?
Просто напиши с чем тебе
нужна помощь
10. Индексный метод в факторном анализе
10. Индексный метод в факторном анализе
В статистике, планировании и анализе хозяйственной деятельности основой для количественной оценки роли отдельных факторов в динамике изменений обобщающих показателей являются индексные модели. Индексный метод – один из приемов элиминирования. Основывается на относительных показателях динамики, пространственных сравнений, выполнении плана, выражающих отношение фактического уровня анализируемого показателя в отчетном периоде к его уровню в базисном периоде (или к плановому, или по другому объекту). Любой индекс исчисляется сопоставлением соизмеряемой (отчетной) величины с базисной. Индексы, выражающие соотношение непосредственно соизмеряемых величин, называются индивидуальными, а характеризующие соотношения сложных явлений – групповыми, или тотальными.
Статистика оперирует различными формами индексов (агрегатная, арифметическая, гармоническая и др.), используемыми в аналитической работе.
Агрегатный индекс является основной формой любого общего индекса; его можно преобразовать как в средний арифметический, так и в средний гармонический индексы. С помощью агрегатных индексов можно выявить влияние различных факторов на изменение уровня результативных показателей в мультипликативных и кратных моделях.
Корректность определения размера каждого фактора зависит от:
1) количества знаков после запятой (не менее четырех);
2) количества самих факторов (связь обратно пропорциональна).
Принципы построения индексов: изменение одного фактора при неизменном значении всех остальных, при этом если обобщающий экономический показатель представляет собой произведение количественного (объемного) и качественного показателей-факторов, то при определении влияния количественного фактора качественный показатель фиксируется на базисном уровне, а при определении влияния качественного фактора количественный показатель фиксируется на уровне отчетного периода.
Пусть Y = а?Ь?с?d. Тогда:

Индексный метод позволяет провести разложение по факторам не только относительных, но и абсолютных отклонений обобщающего показателя. В этом случае влияние отдельных факторов определяется с помощью разности между числителем и знаменателем соответствующих индексов, т. е. также при расчете влияния одного фактора элиминируется влияние другого:
Пусть Y = а?Ь, где а – количественный фактор, ab – качественный. Тогда:
a1?b —a?b – абсолютный прирост результирующего показателя за счет фактора а;
a1?b1 —a1?b – абсолютный прирост результирующего показателя за счет фактора b;
a1?b1 —a?b – абсолютный прирост результирующего показателя за счет влияния всех факторов.
Данный принцип разложения абсолютного прироста (отклонения) обобщающего показателя по факторам пригоден для случая, когда число факторов равно двум (один из них количественный, другой – качественный), а анализируемый показатель представлен как их произведение.
Теория индексов не дает общего метода разложения абсолютных отклонений обобщающего показателя по факторам при числе факторов более двух. Для решения этой задачи используется метод цепных подстановок.
Данный текст является ознакомительным фрагментом.