Анализ случайных чисел

Анализ случайных чисел

АНАЛИЗ ГЕНЕРАТОРА ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ С ПОМОЩЬЮ СТАТИСТИЧЕСКИХ ТЕСТОВ

студенты 3 курса факультета информатики СГАУ им. Академика Королева, РФ, г. Самара

Тишин Владимир Викторович

научный руководитель, доцент, кафедра прикладной математики СГАУ им. академика С.П. Королева, РФ, г. Самара

Генерация случайных чисел — процесс, направленный на получение последовательности независящих друга от друга чисел, подчиняющихся некому закону распределения. Область применения случайных чисел, занимает многие ниши в информационных технологиях.

Выделяют два вида генераторов

· Аппаратный генератор случайных чисел (АГСЧ)

· Генератор псевдослучайных чисел (ГПСЧ)

Аппаратный генератор случайных чисел — некое устройство, генерирующее последовательность случайных чисел, используя характеристики протекающего физического процесса. Работа устройства основывается на использовании накопленных источников энтропии:

По сути, весь окружающий наш мир, это огромный генератор случайных величин. Хоть величины получаются псевдослучайны, но всем этим закономерностям нельзя прописать общий закон, из-за бесконечного множества вариантов развития происходящих событий.

Проблемы, возникающие в данном подходе генерации случайной величины:

· Низкая скорость по сравнению с ГПСЧ

· Короткий срок эксплуатации

Генератор псевдослучайных чисел — генерация случайной величины происходит заданным алгоритмом. В отличие от АГСЧ, где использовалась накопленная энтропия, в данном подходе используется единственное начальное значение. Именно из-за этого подхода, случайная величина в данном случае называется псевдослучайной.

На практике АГСЧ используется чаще всего в исследовательских целях, поэтому в дальнейшем мы будем рассматривать ГПСЧ, из-за его широкого приложения в информационных технологиях и криптографии, а именно:

· Генерация ключей для ассиметричных шифров

· В компьютерном моделировании

· В игровых целях

Одна из проблем ГПСЧ, это появляющиеся проблемы уязвимости:

· Прогнозируемая зависимость между случайными величинами

· Прогнозируемое начальное значение алгоритма

· Слишком короткий период повторения

Например, для моделирования поведения какой-либо случайной величины отлично подойдет такой генератор, обладающий высокой скоростью генерации новых элементов, но для моделирования не обязательна криптографическая стойкость. Для использования в криптографических системах, использующих симметричное или ассиметричное шифрование напротив, криптостойкость ГПСЧ выходит на первое место. В нашей работе мы хотели бы рассмотреть генерацию псевдослучайных последовательностей именно для криптографических систем.

Рассмотрим алгоритм Блюм-Блюма-Шуба и проверим [1]. Генерация нового значения происходит следующим образом:

где: x_n — новый элемент последовательности,

M = p*q, где p и q большие простые числа. Выходными данными на каждом шаге алгоритма являются бит четности x_n или несколько битов наименьшей значимости x_n. На числа p и q накладываются так же дополнительные ограничения, p = q = 3 (mod 4). Это обеспечивает достаточную длину цикла без повторений, что необходимо для генерации достаточного количества псевдослучайных чисел. Еще одно условие, что начальное значение 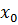должно быть взаимно простым с M. Особенностью данного алгоритма является то, что, зная начальное состояние генератора, а также числа p и q, можно восстановить любой член последовательности, не считая предыдущие (рис. 1).

Благодаря сложности задачи факторизации числа М, невозможно за полиномиальное время подобрать нужные числа p и q, чтобы остановить нужные биты последовательности. То есть, если p и q удовлетворяют всем вышеизложенным условиям, не существует такого полиномиально-временного алгоритма, с помощью которого можно было бы предсказать появление следующего бита с вероятностью более пятидесяти процентов, что обеспечивает криптостойкость алгоритма

Итак, мы имеем алгоритм ГПСЧ, но можно ли сказать, что любая последовательность, получаемая с помощью него, действительно является случайной? Из определения случайно величины: Это величина, принимающая в результате опыта одно из множества значений, и появление ни одного значения нельзя точно предсказать до ее измерения. Таким образом, имея заранее сгенерированную последовательность чисел, стоит задача определить, не являются ли значения в ней связны или принадлежащими к какому-нибудь закону распределения. Для решения этой задачи используют статистические тесты.

Статистические тесты — один из видов тестирования ГПСЧ, который выдает численную характеристику последовательности и позволяет однозначно выявить, пройден ли тест. Многие исследовательские институты и центры составляют и усовершенствуют различные статистические тесты. Наиболее известные:

Для проверки последовательности, полученной с помощью алгоритма Блюм-Блюм-Шуба, мы выбрали тесты NIST, из-за открытого исходного кода всех тестов.

Статистические тесты NIST — пакет статистических тестов, разработанный Национальным институтом стандартов и технологий. В состав пакета входит 15 тестов, определяющих меры случайности двоичных последовательностей полученными с помощью ГПСЧ или АГСЧ. Эти тесты основаны на различных статистических свойствах, присущих только случайным последовательностям. Рассмотрим некоторые из них[3]:

· Частотный побитовый тест — проверка соотношения между нулями и единицами в последовательности и насколько близко доля нулей к 0.5. Если значение вероятности p

Случайные числа не случайны

Как создать генератор случайных чисел на JS и предсказать Math.random()

Вы когда-нибудь задумывались, как работает Math.random()? Что такое случайное число и как оно получается? А представьте вопрос на собеседовании — напишите свой генератор случайных чисел в пару строк кода. И так, что же это такое, случайность и возможно ли ее предсказать.

Генератор псевдослучайных чисел и генератор случайных чисел

Для того, чтобы получить что-то случайное, нам нужен источник энтропии, источник некого хаоса из который мы будем использовать для генерации случайности.

Этот источник используется для накопления энтропии с последующим получением из неё начального значения (initial value, seed), которое необходимо генераторам случайных чисел (ГСЧ) для формирования случайных чисел.

Генератор ПсевдоСлучайных Чисел использует единственное начальное значение, откуда и следует его псевдослучайность, в то время как Генератор Случайных Чисел всегда формирует случайное число, имея в начале высококачественную случайную величину, которая берется из различных источников энтропии.

Энтропия — это мера беспорядка. Информационная энтропия — мера неопределённости или непредсказуемости информации.

Выходит, что чтобы создать псевдослучайную последовательность нам нужен алгоритм, который будет генерить некоторую последовательность на основании определенной формулы. Но такую последовательность можно будет предсказать. Тем не менее, давайте пофантазируем, как бы могли написать свой генератор случайных чисел, если бы у нас не было Math.random()

ГПСЧ имеет некоторый алгоритм, который можно воспроизвести.
ГСЧ — это получение чисел полностью из какого либо шума, возможность просчитать который стремится к нулю. При этом в ГСЧ есть определенные алгоритмы для выравнивания распределения.

Придумываем алгоритм ГПСЧ

Генератор псевдослучайных чисел (ГПСЧ, англ. pseudorandom number generator, PRNG) — алгоритм, порождающий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному).

Мы можем взять последовательность каких-то чисел и брать от них модуль числа. Самый простой пример, который приходит в голову. Нам нужно подумать, какую последовательность взять и модуль от чего. Если просто в лоб от 0 до N и модуль 2, то получится генератор 1 и 0:

Эта функция генерит нам последовательность 01010101010101… и назвать ее даже псевдослучайной никак нельзя. Чтобы генератор был случайным, он должен проходить тест на следующий бит. Но у нас не стоит такой задачи. Тем не менее даже без всяких тестов мы можем предсказать следующую последовательность, значит такой алгоритм в лоб не подходит, но мы в нужном направлении.

А что если взять какую-то известную, но нелинейную последовательность, например число PI. А в качестве значения для модуля будем брать не 2, а что-то другое. Можно даже подумать на тему меняющегося значения модуля. Последовательность цифр в числе Pi считается случайной. Генератор может работать, используя числа Пи, начиная с какой-то неизвестной точки. Пример такого алгоритма, с последовательностью на базе PI и с изменяемым модулем:

Но в JS число PI можно вывести только до 48 знака и не более. Поэтому предсказать такую последовательность все так же легко и каждый запуск такого генератора будет выдавать всегда одни и те же числа. Но наш генератор уже стал показывать числа от 0 до 9. Кстати, так выглядит распределение по выпадению чисел при 10000 итерациях:

Распределение очень неравномерное, но мы получим генератор чисел от 0 до 9.

Мы можем взять не число Pi, а время в числовом представлении и это число рассматривать как последовательность цифр, причем для того, чтобы каждый раз последовательность не повторялась, мы будем считывать ее с конца. Итого наш алгоритм нашего ГПСЧ будет выглядеть так:

Вот это уже похоже на генератор псевдослучайных чисел. И тот же Math.random() — это ГПСЧ, про него мы поговорим чуть позже. При этом у нас каждый раз первое число получается разным.

Собственно на этих простых примерах можно понять как работают более сложные генераторы случайных числе. И есть даже готовые алгоритмы. Для примера разберем один из них — это Линейный конгруэнтный ГПСЧ(LCPRNG).

Линейный конгруэнтный ГПСЧ

Линейный конгруэнтный ГПСЧ(LCPRNG) — это распространённый метод для генерации псевдослучайных чисел. Он не обладает криптографической стойкостью. Этот метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой следующей формулой:

где a(multiplier), c(addend), m(mask) — некоторые целочисленные коэффициенты. Получаемая последовательность зависит от выбора стартового числа — т.е. seed. При разных значениях seed получаются различные последовательности случайных чисел. Пример реализации такого алгоритма на JavaScript:

Многие языки программирования используют LСPRNG (но не именно такой алгоритм(!)).

Как говорилось выше, такую последовательность можно предсказать. Так зачем нам ГПСЧ? Если говорить про безопасность, то ГПСЧ — это проблема. Если говорить про другие задачи, то эти свойства — могут сыграть в плюс. Например для различных спец эффектов и анимаций графики может понадобиться частый вызов random. И вот тут важны распределение значений и перформанс! Секурные алгоритмы не могут похвастать скоростью работы.

Еще одно свойство — воспроизводимость. Некоторые реализации позволяют задать seed, и это очень полезно, если последовательность должна повторяться. Воспроизведение нужно в тестах, например. И еще много других вещей существует, для которых не нужен безопасный ГСЧ.

Как устроен Math.random()

Метод Math.random() возвращает псевдослучайное число с плавающей запятой из диапазона [0, 1) , то есть, от 0 (включительно) до 1 (но не включая 1), которое затем можно отмасштабировать до нужного диапазона. Реализация сама выбирает начальное зерно для алгоритма генерации случайных чисел; оно не может быть выбрано или сброшено пользователем.

Как устроен алгоритм Math.random() — интересный вопрос. До недавнего времени, а именно до 49 Chrome использовался алгоритм MWC1616:

Именно этот алгоритм генерит нам последовательность псевдослучайных чисел в промежутке между 0 и 1.

UPD

Исправил ошибку в алгоритме MWC1616 (пропущенные скобки). Эта же ошибка повторяется и в статье https://v8project.blogspot.ru/2015/12/theres-mathrandom-and-then-theres.html

то видим, что должны быть скобки:

Предсказываем Math.random()

Чем это было чревато? Есть такой квест: https://alf.nu/ReturnTrue

В нем есть задача:

Что нужно вписать вместо вопросов, чтобы функция вернула true? Кажется что это невозможно. Но, это возможно, если вы заглядывали в спеку и видели алгоритм ГПСЧ V8. Решение этой задачи в свое время мне показал Роман Дворнов:

Этот код работал в 70% случаев для Chrome

Видите эти равномерности на левом слайде? Изображение показывает проблему с распределением значений. На картинке слева видно, что значения местами сильно группируются, а местами выпадают большие фрагменты. Как следствие — числа можно предсказать.

Выходит что мы можем отреверсить Math.random() и предсказать, какое было загадано число на основе того, что получили в данный момент времени. Для этого получаем два значения через Math.random(). Затем вычисляем внутреннее состояние по этим значениям. Имея внутреннее состояние можем предсказывать следующие значения Math.random() при этом не меняя внутреннее состояние. Меняем код так так, чтобы вместо следующего возвращалось предыдущее значение. Собственно все это и описано в коде-решении для задачи random4. Но потом алгоритм изменили (подробности читайте в спеке). Его можно будет сломать, как только у нас в JS появится нормальная работа с 64 битными числами. Но это уже будет другая история.

Новый алгоритм выглядит так:

Его все так же можно будет просчитать и предсказать. Но пока у нас нет “длинной математики” в JS. Можно попробовать через TypedArray сделать или использовать специальные библиотеки. Возможно кто-то однажды снова напишет предсказатель. Возможно это будешь ты, читатель. Кто знает 😉

Инструмент анализа «Генерация случайных чисел»

Для описания реальных случайных процессов и их результатов часто используются рассчитыва­емые на ЭВМ «имитационные модели». Данные для расчёта этих моделей должны быть получены в результате генерации случайных величин. При «ручном» построении имитационной модели эти данные берутся из известных справочных таблиц случайных чисел. В них числа обычно представлены как незави­симые реализации или выборки случайной величины, равно­мерно распределенной, например, на единичном интервале [0, 1], полученные путём простого случайного выбора из совокупности цифр.

Но параметры реальных производственных процессов или характеристики качества далеко не всегда распределены равно­мерно (см. § 4.2). Использование современных программных средств позволяет преодолеть данное противоречие: получить последовательности слу­чайных величин, имеющих различные законы распределения. С помощью данной процедуры можно моделировать объекты, имеющие случайную природу, по известному распределению ве­роятностей.

В пакете «Анализ данных» инструмент «Генерация случайных чи­сел», рис. 5.12, используется для заполнения выбранного диапазона значений случайными числа­ми, извлеченными из одного или нескольких распределений.

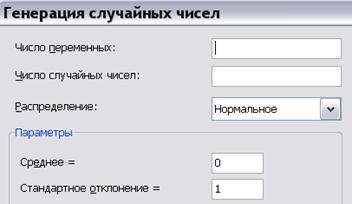
Рис. 5.12. Инструмент анализа «Генерация случайных чисел»

При этом для непрерывных величин предлагаются два вида распределения:

1. Равномерное. Характеризуется верхней и нижней границами. По умолчанию равномерное распределение используют в интервале [0, 1]. Случайные величины извлекаются с одной и той же вероятностью для всех значений выбранного интервала (дублируются возможности справочных таблиц случайных чисел, см. выше).

2. Нормальное. В отличие от предыдущего вероятность распределения извлечённых случайных величин подчиняется не равномерному, а нормальному закону, то есть чем ближе расположены числа к среднему 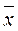, тем с большей вероятностью они извлекаются числа. Характеризуется средним значением и стандартным отклонением. По умолчанию производится генерация случайных чисел для стандартного нормального распределения: 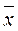= 0, σ = 1.

Для дискретных величин предлагаются следующие виды распределения:

— Модельное, характеризующееся нижней и верхней границами, шагом, числом повторений значений и числом повторений последовательности.

— Дискретное, характеризующееся значением и соответствующим ему интервалом вероятности. Диапазон должен состоять из двух столбцов: левого, содержащего значения, и правого, содержащего вероятности, связанные со значением в данной строке. Сумма вероятностей должна быть равна 1.

Аргументы окна инструмента «Генерация случайных чисел»:

— «Число переменных», при помощи которого можно получить многомерную выборку. Для этого необходимо ввести число столбцов таблицы входных данных.

— «Число случайных чисел» определяет число точек данных (число реализаций), которое необходимо генерировать для каждой переменной. Каждое случайное значение будет помещено в соответствующей строке выходного диапазона.

— «Распределение» служит для выбора нужного закона распределения случайных чисел.

— «Параметры» служит для введения пара­метров для каждого из выбранных законов распределения и различается в зависимости от выбранного закона. Для нормального закона, см. рис. 5.12, вводятся среднее значение и стандартного отклонения, а для равномерного распределения — максимальное и минимальное значение.

Аргумент «Случайное рассеивание» служит для введения произвольного значения, для которого необходимо генерировать случайные числа. Excel «запоминает» соответствие сгенерированной совокупно­сти случайных чисел введенному произвольному числу. Впоследствии можно снова использовать это значение для получения той же самой совокупности случайных чисел. Если никакое число не введено, то каждая сгенерированная совокупность случай­ных чисел будет индивидуальна.

Генерация случайных чисел

Рис. 6.26. Окно надстройки Анализ данных

В списке Инструменты анализа необходимо выбрать позицию Генерация случайных чисел и щелкнуть на кнопке OK. Настройки по генерации случайных чисел выполняются в окне Генерация случайных чисел. Главным функциональным элементом в этом окне является, пожалуй, раскрывающийся список Распределение. В этом раскрывающемся списке выбирается тип распределения случайной величины, на основе которого генерируются случайные числа. Всего в списке семь позиций, названия которых соответствуют основным, наиболее часто используемым на практике распределениям. Доступные типы распределений представлены в табл. 6.17. Там же приведена краткая справка по каждому из распределений и показан вид диалогового окна Генерация случайных чисел для выбранного распределения, описаны настройки, специфичные для данного распределения. Общие настройки описаны далее.
Отредактировал и опубликовал на сайте ¦ PRESSI ( HERSON )
U Анализ данных
Фильтр
Очистить
Применить повторно
..».^Дополнительно ртировка ні фильтр
Текст пю Удалить ^ столбцам дубликаты Работа сданными
Структура
иск решения Средства для анализа данных
Средства для анализа финансовых и научных данных, G н 1 і @ FUNCRE5.XLAM Для получения дополнительных сведений нажмите клавишу F1,

Рис. 6.25. Запуск надстройки Пакет анализа

Таблица 6.17. Распределения для генерации случайных чисел
Распределение
Описание
Вид диалогового окна
Равномерное распределение

Случайная величина, равномерно распределенная на интервале (a, b) характери-зуется плотностью распределения f (x) = 1/(b — a) при x є (a, b) и f (x) = 0 при x t (a, b). Для этого типа распределения указываются границы интервала, на котором распреде-лена случайная величина. Границы интервала указываются в полях Между. и.
Jjxj
Плотность нормального распределения определяется как
ґ (x — a)2 ^
exp
2a2
f (x) = —
n/2to
na

Случайная величина принимает два значения: 1 (успех) с вероятностью p и 0 (неудача) с вероятностью q = 1 — p.

Для генерации случайных чисел в поле Значение р= указывается вероятность успехаp
где а является математическим ожиданием, а a2 есть дисперсия случайной величины, a — стандартное отклонение. Значение параметра a указывается в поле Среднее=, а стандартное отклонение водится в поле Стандартное отклонение=
Нормальное распределение
Генерация случайный 1
Число переменных: Число случайных чисел: |
Распределение: |нормальное
-Параметры
Среднее —
Стандартное отклонение =
Случайное рассеивание:
-Параметры вывода
Распределение Бернулли
Выходной интервал: (• Новый рабочий пнет: | С Новая рабочая книга
Таблица 6.17 (продолжение)
Распределе-
Описание
ние
Вид диалогового окна
Jjxj
3
Биномиальное
Биномиальное распределение характеризуется законом для вероятности реализации случайной величины ? со значением m вида P (? = m) = Cmpmqn-m. Такая случайная величина может интерпретироваться как число успехов в серии из n независимых испытаний с вероятностью успеха в одном испытании p, а q = 1 — p есть вероятность неудачи в одном опыте. В поле Значение р= указывается вероятностью успеха в одном испытании p, а число испытаний в серии n вводится в поле Число испытаний=
Биномиальное распределение
Число переменных: Число случайных чисел: Распределение:
-Параметры
Значение р — Число испытаний =
Случайное рассеивание:
-Параметры вывода
Ґ» Выходной интервал: Г