Экономические задачи методом анализа иерархий
Метод анализа иерархий
Назначение . С помощью онлайн-калькулятора производятся вычисление коэффициентов важности для элементов каждого уровня — индексы однородности и отношения однородности.
- Решение онлайн
- Видеоинструкция
- Оформление Word
Таблица 2. Шкала отношений
Теорема 1 . В положительной обратносимметрической квадратной матрице λmax≥n.
Теорема 2 . Положительная обратносимметрическая квадратная матрица А согласованна тогда и только тогда, когда λmax=n.
Таким образом, для оценки однородности суждений эксперта можно использовать отклонение величины максимального собственного значения λmax от порядка матрицы n.
Согласованность суждения оценивается индексом однородности (индексом согласованности) или отношением однородности (отношением согласованности) в соответствии со следующими формулами:
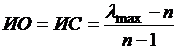
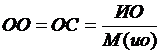
M(ио) — среднее значение индекса однородности случайным образом составленной матрицы парных сравнений, которое основано на экспериментальных данных. Значение есть табличная величина, входным параметром выступает размерность матрицы (таблица 6).
Таблица 6. Среднее значение индекса однородности в зависимости от порядка матрицы
Пример . Рассмотрим матрицу парных сравнений и вычислим приближенное значение главного собственного вектора:
Просуммируем элементы каждой строки и найдем сумму всех элементов матрицы:
Нормализуя вектор Ws делением каждой координаты на величину S, получаем приближенное значение главного собственного вектора:
Приближенное значение максимального собственного значения можно найти по формуле λmax=e T AW, рассмотренной выше:
При таком вычислении главного собственного вектора и максимального собственного значения может оказаться, что согласованная в действительности матрица является несогласованной по вычислениям и наоборот.
Пример . Вычислим отношение согласованности рассматриваемой выше матрицы, взяв в качестве максимального собственного значения его точное и приближенное число.
При большей погрешности метода вычисления главного собственного вектора, отношение согласованности матрицы парных сравнений могло оказаться больше 0.01 .
Желательно использовать процедуры точного нахождения собственных значений и векторов матриц. Такое пожелание превращается в требование в особо ответственных задачах.
Пример (из книги Т. Саати). Рассмотрим общее благополучие индивидуума – высший уровень иерархии. На этот уровень в основном влияют детские, юношеские и взрослые впечатления. Факторы развития и зрелости, отражающиеся в благополучии, могут включать как влияние отца и матери в отдельности, так и их совместное влияние как родителей, социоэкономический фон, отношения с братьями и сестрами, группу ровесников, школьное обучение, религиозный статус и т.д.
На перечисленные выше факторы, которые составляют второй уровень иерархии, влияют соответствующие критерии. Например, влияние отца может быть разбито на категории, включающие его темперамент, строгость, заботу и привязанность. Отношение с братьями и сестрами можно дальше характеризовать их количеством, разницей в возрасте, полом; моделирование воздействия и роли ровесников обеспечивает более яркую картину влияния друзей, обучения в школе и учителей.
В качестве альтернативной основы описания для второго уровня можно включить чувство собственного достоинства, уверенность в будущем, адаптируемость к новым людям и новым обстоятельствам и т.д., влияющих или находящихся под влиянием расположенных выше элементов.
Более полная основа психологической предыстории может включать несколько сотен элементов на каждом уровне, выбранных экспертами и расположенных таким образом, чтобы получить максимальное понимание рассматриваемого индивидуума.
Рассмотрим ограниченный случай, где испытуемый чувствует, что уверенность в его силы подорвана и его социальная приспособляемость ослаблена запретами в детстве. Ему задают вопросы только о детских впечатлениях и просят попарно установить связь между следующими элементами на каждом уровне.
Построим иерархию, в которой: ОБ – общее благополучие; Д – чувство собственного достоинства; У – чувство уверенности в будущем; А – способность адаптироваться к другим; П – явная привязанность, проявленная по отношению к субъекту; Э – идеи строгости, этики; Н – действительное наказание ребенка; Л – подчеркивание личной приспособляемости к другим; М – влияние матери; О – влияние отца; Р – влияние обоих родителей.
Рисунок 1 — Иерархическая схема общего благополучия индивидуума
WОБ=(0.701; 0.193; 0.106), λmax=3.26; ИС=0.07; OC=0.12
WД=(0.604; 0.213; 0.064; 0.119), λmax=4.35; ИС=0.12; OC=0.13
WУ=(0.604; 0.213; 0.064; 0.119), λmax=4.35; ИС=0.12; OC=0.13
WA=(0.127; 0.281; 0.120; 0.463), λmax=5.42; ИС=0.47; OC=0.52
WП=(0.721; 0.210; 0.069), λmax=4; ИС=0.33; OC=0.57
WЭ=(0.333; 0.333; 0.333), λmax=3; ИС=0.0; OC=0.0
WН=(0.713; 0.061; 0.176), λmax=3.11; ИС=0.06; OC=0.10
WЛ=(0.701; 0.097; 0.202; 0.463), λmax=3.14; ИС=0.07; OC=0.12
Осуществим иерархический синтез:
Индивидууму посоветовали больше общаться с отцом с целью уравновешивания влияния родителей.
В приведенном примере некоторые матрицы несогласованные. Однако следует понимать, что человеку в данной ситуации нельзя было повторно задавать одни и те же вопросы до тех пор, пока все матрицы не стали бы однородными.
После решения задачи синтеза иерархии, оценивается однородность всей иерархии с помощью суммирования показателей однородности всех уровней, приведенных путем взвешивания к первому иерархическому уровню.
Экономические задачи методом анализа иерархий
Во все времена существования отечественной высшей школы проблема поиска объективных и достоверных критериев, достаточно полно определяющих эффективность труда преподавателей, постоянно находилась в центре внимания организаторов учебного процесса и вузовской общественности. Деятельность преподавателя многогранна. По официальной отчетности она охватывает учебную, учебно-методическую, научно-исследовательскую, организационно-методическую и воспитательную работу. Можно выделить достаточно много количественных показателей, характеризующих каждый вид деятельности преподавателя, использование которых учитывается при определении рейтинговой оценки его работы [4, 8, 9]. Но чрезмерное количество показателей усложняет систему подсчета рейтинга профессорско-преподавательского состава (ППС) и далеко не всегда способствует повышению объективности оценки его труда.
Одним из таких показателей, позволяющим проверить качество учебного процесса преподавателя, является оценка его работы по результатам текущей успеваемости и посещаемости студентов. Чтобы учесть многообразие критериев оценки текущей успеваемости, создаются различные алгоритмы, методы, способы, подходы. Предлагаемый подход оценки качества процесса управления работой преподавателя использует возможности применения информационных технологий [5]. Например, алгоритм оценки работы преподавателя может базироваться на методе анализа иерархии Саати.
1. Метод анализа иерархий Саати
Метод анализа иерархий (МАИ) состоит в иерархической декомпозиции проблемы на все более простые составляющие части и дальнейшей обработке последовательности суждений эксперта по парным сравнениям [6].
В общем случае иерархическая модель может быть представлена следующим образом: (рис. 1): на самом верхнем уровне находится глобальная цель (фокус иерархии), продолжается к критериям, далее к подкритериям и так далее до самого нижнего уровня – альтернатив.
После формирования иерархии критериев оценки устанавливаются приоритеты (веса) критериев и в соответствии с ними производится оценка альтернатив по методу линейной свертки. В результате определяется относительная значимость исследуемых альтернатив для всех критериев, находящихся в иерархии.
На основании суждений эксперта строятся матрицы парных сравнений на каждом уровне по отношению к каждому критерию вышестоящего уровня.
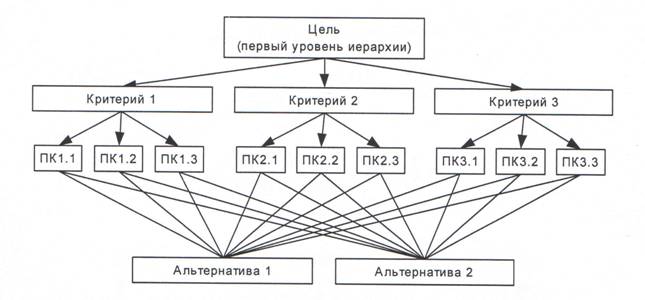
Рис. 1. Иерархическая модель по МАИ Саати
Можно выделить ряд модификаций МАИ, которые определяются характером связей между критериями и альтернативами, расположенными на самом нижнем уровне иерархии, а также методом сравнения альтернатив [7]. По характеру связей между критериями и альтернативами определяется два типа иерархий. К первому типу относятся такие, у которых каждый критерий, имеющий связь с альтернативами, связан со всеми рассматриваемыми альтернативами (тип иерархий с одинаковыми числом и функциональным составом альтернатив под критериями). Ко второму типу иерархий принадлежат те, у которых каждый критерий, имеющий связь с альтернативами, связан не со всеми рассматриваемыми альтернативами (тип иерархий с различными числом и функциональным составом альтернатив под критериями).
При принятии управленческих решений и прогнозировании возможных результатов эксперт, принимающий решение, обычно сталкивается со сложной системой взаимозависимых компонент (таких как ресурсы, желаемые исходы или цели, лица или группа лиц и т.д.), которую нужно проанализировать [3].
Таким образом, метод анализа иерархий Саати проводится по следующей схеме [6, 7]:
— структурирование проблемы выбора в виде иерархии или сети;
— установка приоритетов критериев и оценка каждой из альтернатив по критериям;
— определение коэффициентов важности для элементов каждого уровня;
— подсчет комбинированного весового коэффициента и определение наилучшей альтернативы.
2. Применение метода анализа иерархий в оценке качества работы преподавателей
Иерархическая модель оценки работы преподавателя может быть представлена следующим образом (рис. 2): на самом верхнем уровне находится глобальная цель (качество работы преподавателя); продолжается к критериям – успеваемость и посещаемость студентов; далее к подкритериям, описывающим конкретные показатели работы преподавателя.
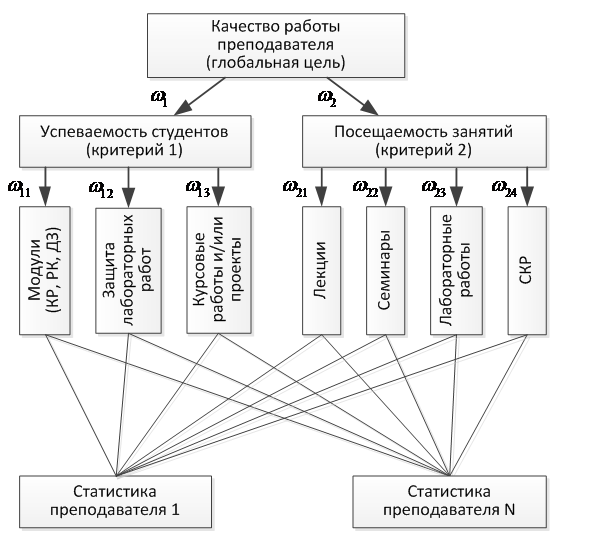
Рис. 2. Иерархическая модель оценки работы преподавателя
На рисунке 2 обозначены: модули – контрольные работы (КР), рубежные контроли (РК), домашние задания (ДЗ), СКР – самостоятельная контролируемая работы студентов; w1, w2– веса критериев; w11,…, w24 – веса подкритериев.
После формирования иерархии критериев оценки (успеваемость и посещаемость) и подкритериев (для успеваемости – модули, защита лабораторных работ, курсовые работы/проекты; для посещаемости – лекции, практические занятия (семинары), лабораторные работы, СКР) устанавливаются веса критериев и в соответствии с ними производится оценка альтернатив – преподавателей, осуществляющих учебный процесс.
Веса критериев устанавливаются на основе экспертной оценки, осуществляемой, например, представителями кафедр вуза. Для этого необходимо осуществить парное сравнение критериев друг с другом по их важности – вкладу в глобальную цель.
На основании суждений эксперта строятся матрицы попарных сравнений на каждом уровне по отношению к каждому критерию вышестоящего уровня.
При сравнении двух объектов по какому-либо критерию эксперт пользуется заранее определенной девятибалльной шкалой (табл. 1) [6]. Выбор такой школы обусловлен следующими причинами [6].
1. Качественные различия значимы на практике и обладают элементом точности, когда величины сравниваемого показателя для обоих вариантов являются величинами одного порядка или когда они близки относительно свойства, использованного для сравнения.
2. Способность человека производить качественные различия хорошо представлена пятью определениями: равный, слабый, сильный, очень сильный, абсолютный. Можно принять компромиссные решения между соседними определениями, когда требуется большая точность.
Девятибалльная шкала, используемая в методе анализа иерархий
3.3 Применение метода анализа иерархий для определения стратегии повышения экономической устойчивости предприятия
Метод Анализа Иерархий (МАИ) — математический инструмент системного подхода к сложным проблемам принятия решений.
МАИ не предписывает лицу, принимающему решение, какого-либо «правильного» решения», а позволяет ему в интерактивном режиме найти такой вариант (альтернативу), который наилучшим образом согласуется с его пониманием сути проблемы и требованиями к ее решению.
МАИ позволяет понятным и рациональным образом структурировать сложную проблему принятия решений в виде иерархии, сравнить и выполнить количественную оценку альтернативных вариантов решения.
Анализ проблемы принятия решений в МАИ начинается с построения иерархической структуры, которая включает цель, критерии, альтернативы и другие рассматриваемые факторы, влияющие на выбор.
Эта структура отражает понимание проблемы лицом, принимающим решение. Каждый элемент иерархии может представлять различные аспекты решаемой задачи, причем во внимание могут быть приняты как материальные, так и нематериальные факторы, измеряемые количественные параметры и качественные характеристики, объективные данные и субъективные экспертные оценки. Иными словами, анализ ситуации выбора решения в МАИ напоминает процедуры и методы аргументации, которые используются на интуитивном уровне.
Следующим этапом анализа является определение приоритетов, представляющих относительную важность или предпочтительность элементов построенной иерархической структуры, с помощью процедуры парных сравнений. Безразмерные приоритеты позволяют обоснованно сравнивать разнородные факторы, что является отличительной особенностью МАИ.
На заключительном этапе анализа выполняется синтез (линейная свертка) приоритетов на иерархии, в результате которой вычисляются приоритеты альтернативных решений относительно главной цели. Лучшей считается альтернатива с максимальным значением приоритета.
Постановка задачи: в результате проведенного анализа была прослежена тенденция снижения уровня экономической устойчивости предприятия, что отобразилось в уменьшении показателей рентабельности, оборачиваемости, финансовой устойчивости, а также в увеличении вероятности наступления банкротства. Для того, чтобы выйти из сложившегося затруднительного положения, предприятию необходимо предпринять ряд мер, направленных на повышения уровня экономической устойчивости, т.е. выработать стратегию финансового развития.
Предприятие может рассматривать следующие стратегии:
1) стратегия снижения кредиторской задолженности;
2) стратегия сокращения незавершенного производства;
3) стратегия повышения выручки от реализации;
4) стратегия сокращения дебиторской задолженности;
5) стратегия сокращения величины материальных запасов.
Дерево целей и решений представлено на рисунке 6.
Рисунок 6 – Дерево целей и решений
Матрица оценок попарного сравнения альтернатив используется для построения иерархии целей путем ответа на вопрос: какая из каждых двух сравниваемых подцелей важнее для достижения цели более высокого уровня.
Путем порядковой оценки определяется, какая из каждых двух сравниваемых стратегий предпочтительнее для наилучшего достижения поставленной цели.
Полученные данные попарного сравнения сценариев, целей и стратегий оформляются в виде матриц.
Шкала попарного сравнения альтернатив представлена в таблице 18.
Таблица 18 — Шкала попарного сравнения альтернатив
