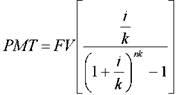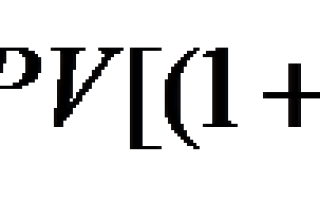Накопление денежной единицы за период это
Шесть функций денежной единицы.
Для определения стоимости инвестиционного проекта или собственности необходимо определить текущую стоимость денег, которые будут получены через некоторое время в будущем. В условиях инфляции деньги изменяют свою стоимость с течением времени. Основными операциями, позволяющими сопоставить разновременные деньги являются операции накопления (наращивания) и дисконтирования.
Накопление – это процесс приведения текущей стоимости денег к их будущей стоимости при условии, что вложенная сумма будет находиться на счету в течение определенного времени, принося периодически накапливаемый процент.
Дисконтирование – процесс приведения денежных поступлений от инвестиций к их текущей стоимости.
1 функция. Определим будущую стоимость денежной единицы (накопленная сумма денежных единиц)
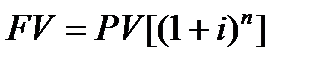
FV — будущая стоимость денежной единицы,
PV – текущая стоимость денежной единицы,
i – ставка дохода,
n – число периодов накопления в годах.
Задача. Определить какая сумма будет накоплена на счете к концу 3 года, если сегодня положить на счет под 10 % годовых 10 тыс. руб.
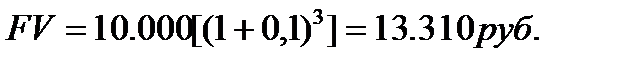
2 функция. Текущая стоимость денежной единицы (текущая стоимость реверсии перепродажи)
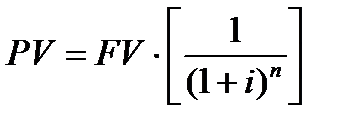
Задача. Сколько нужно вложить сегодня в инвестиционный проект, чтобы к концу 5 года получить 8 тыс.руб. Ставка дохода 10%.
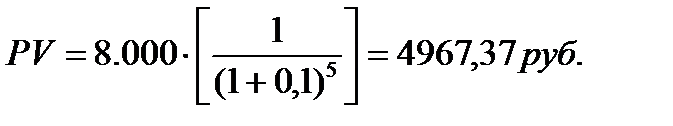
3 функция. Определение текущей стоимости аннуитета.
Аннуитет – это серия равновеликих платежей (поступлений), отстоящих друг от друга на один и тот же промежуток времени.
Выделяют обычный и авансовый аннуитет. Если платежи осуществляют в конце каждого периода, то аннуитет обычный; если вначале – авансовый.
Формула текущей стоимости обычного аннуитета:
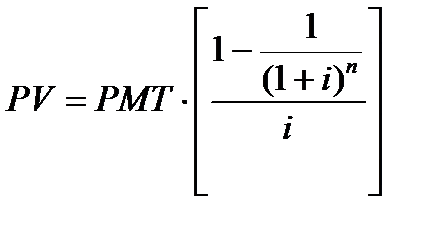
PMT – равновеликие периодические платежи.
Задача. Договор аренды дачи составлен на 1 год. Платежи осуществляются ежемесячно по 1 тыс.руб. Определить текущую стоимость арендных платежей при 12% ставке дисконтирования. n = 12 (число периодов – месяцев).
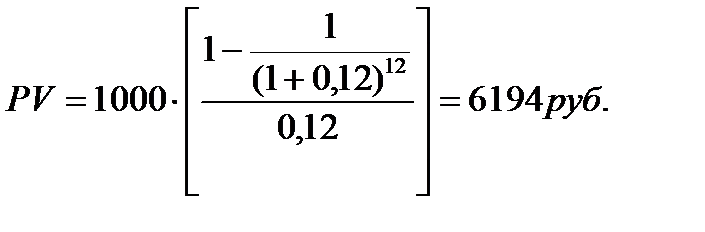
4 функция. Накопление денежной единицы за период. В результате использования данной функции определяется будущая стоимость серии равновеликих периодических платежей или поступлений.
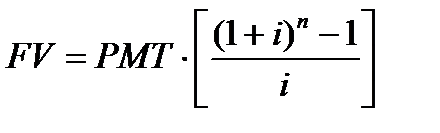
Задача. Определить сумму, которая будет накоплена на счете, приносящем 12% годовых, к концу 5 года, если ежегодно откладывать на счет 10 тыс.руб.
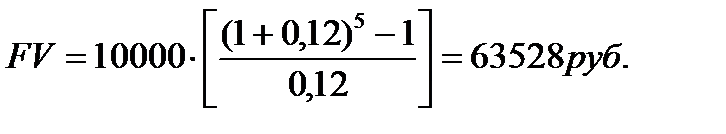
5 функция. Взнос на амортизацию денежной единицы.
Данная функция является обратной величиной текущей стоимости обычного аннуитета.
Амортизация – это процесс, определяемый данной функцией, и включает проценты по кредиту и оплату основной суммы долга.
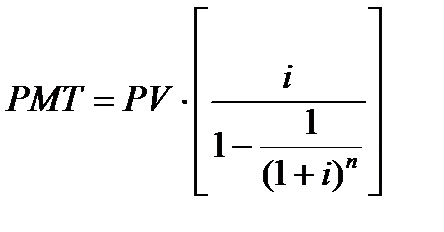
Задача. Определить, какими должны быть ежегодные платежи, чтобы к концу 7 года погасить кредит 100 000 руб., выданный под 15% годовых.
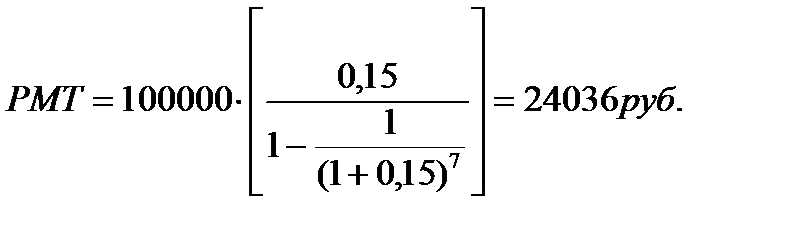
Аннуитет может быть как поступлением (входящим денежным потоком), так и платежом (исходящим денежным потоком), по отношению к инвестору. Поэтому данная функция может быть использована в случае расчета величины равновеликого взноса на погашение кредита при известном числе взносов и заданной процентной ставке. Такой кредит называется самоамортизирующийся кредит.
6 функция. Рассматривает фактор фонда размещения и является обратной функции накопления единицы за период.
Для определения величины платежа используется следующая формула:
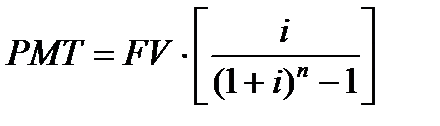
Задача. Определить, какими должны быть платежи, чтобы к концу 5 года иметь на счете при ставке 12% годовых 100 000 руб.
Текущая стоимость аннуитета.
Показывает стоимость равномерного потока платежей на сегодняшний день (аннуитета). Первое поступление в этом потоке осуществляется в конце первого периода, а последующие – в конце каждого из последующих периодов.

Пример: необходимо определить величину кредита, в погашение которого ежеквартально вносится по 35 000,00 руб. в течение 6 лет при ставке 16%.
Решение:
1. Количество периодов (кварталов): n = 6 × 4 = 24
2. Квартальная процентная ставка: i = 16 : 100 : 4 = 0,04
3. Применяем основную формулу: 
Взнос на амортизацию денежной единицы.
Показывает размер равновеликого периодического платежа, необходимого для полной амортизации займа, по которому выплачивается процент.

Пример: в каком размере необходимо вносить ежемесячные платежи по самоамортизирующемуся кредиту в 500 000,00 рублей, предоставленному на 8 лет при годовой ставке в 13%?
Решение:
1. Количество периодов (месяцев): n = 8 × 12 = 96
2. Месячная процентная ставка: i = 13 : 100 : 12 = 0,011
3. Применяем основную формулу: 
Функция сложного процента — накопление денежной суммы за период.
Накопление денежной единицы за период. В результате использования данной функции определяется будущая стоимость серии равновеликих периодических платежей или поступлений.
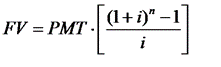
Задача. Определить сумму, которая будет накоплена на счете, приносящем 12% годовых, к концу 5 года, если ежегодно откладывать на счет 10 тыс.руб.

Функция сложного процента — фактор фонда возмещения.
Данная функция обратна функции накопления единицы за период. Фактор фонда возмещения показывает аннуитетный платеж, который необходимо депонировать под заданный процент в конце каждого периода для того, чтобы через заданное число периодов получить искомую сумму.
Для определения величины платежа используется формула:

При платежах (поступлениях), осуществляемых чаще, чем 1 раз в год:

Примером. Определить, какими должны быть платежи, чтобы к концу 5го го да иметь на счете, приносящем 12% годовых, 100 000 рублей. Платежи осуществляются в конце каждого года.

Аннуитетный платеж, определяемый данной функцией, включает выплату основной суммы без выплат процента.
Инфляция. Показатели, характеризующие инфляцию.
Инфля́ция (лат. inflatio — вздутие) — повышение общего уровня цен на товары и услуги. При инфляции на одну и ту же сумму денег по прошествии некоторого времени можно будет купить меньше товаров и услуг, чем прежде. В этом случае говорят, что за прошедшее время покупательная способность денег снизилась, деньги обесценились — утратили часть своей реальнойстоимости.
Показатели.
Формула Фишера.
Уравнение Фишера (также называемое эффектом Фишера и гипотезой Фишера) — уравнение, описывающее связь между темпом инфляции, номинальной и реальной ставками процента: i = r + п,
Содержание и функции финансов предприятия.
Финансы предприятий (организаций) — это относительно самостоятельная сфера системы финансов, охватывающая широкий круг денежных отношений, связанных с формированием и использованием капитала, доходов, денежных фондов предприятий в процессе кругооборота их средств и выраженных в виде различных денежных потоков.
Поэтому финансы предприятий— это совокупность денежных отношений, возникающих у субъектов хозяйствования по поводу формирования фактических и (или) потенциальных фондов денежных средств, их распределения и использования на нужды производства и потребления.
Одним из основных компонентов финансово-хозяйственной деятельности предприятия являются денежные отношения, которые сопутствуют практически всем аспектам деятельности предприятия. Эти отношения возникают между:
· предприятиями при оплате поставок сырья, материалов, топлива, комплектующих, оборудования, запасных частей, инструментов, реализации готовой продукции, формировании и распределении валовой прибыли, взыскании штрафных санкций и т. п.;
· предприятиями при выпуске и распространении их ценных бумаг, паев, взаимном кредитовании, долевом участии в создании предприятий с участием иностранного капитала;
· предприятиями, рабочими и служащими в процессе использования чистой прибыли, при выпуске акций, распространяемых между членами трудового коллектива, выплате дивидендов по акциям;
· предприятиями и государством по поводу образования и использования бюджетных и внебюджетных фондов;
· предприятиями и страховыми организациями в связи с формированием и использованием различного рода страховых фондов;
· предприятиями и банковской системой при получении и погашении банковских ссуд и уплате процентов по ним, предоставлении банкам во временное пользование свободных денежных средств и т. п.;
· предприятиями и вышестоящими организациями, ассоциациями, концернами, внешними собственниками имущества по перераспределению финансовых ресурсов.
Расчет накопления денежной единицы за период;
Фактор накопления денежной единицы за период показывает рост сберегательного счета, на который с равной периодичностью вносится определенная сумма. Деньги на депозите в течение периода приносят процент. Расчет ведут по формуле
Где FV – будущая стоимость сегодняшнего актива;
РМТ – единовременный денежный платеж в этом периоде;
i – обычная ставка процента;
n – число периодов;
Конечную (будущую) сумму FV вычисляют для обычного аннуитета в день последнего вложения.
Пример 1. Вкладчик депонирует 50000 рублей в конце каждого года в течение 5 лет при ставке 10% и ежегодном накоплении. Какая сумма накопится к концу пятого года?
50000 рублей, депонированные в конце первого года, будут приносить проценты в течение последующих четырех лет;
50000 рублей, депонированные по окончании второго года, будут приносить проценты в течение последующих трех лет;
50000 рублей, депонированные в конце третьего года, будут приносить проценты в течение последующих двух лет;
50000 рублей, депонированные в конце четвертого года, будут приносить проценты в течение одного года;
И, наконец, 50000 рублей, депонированные в конце пятого года, не принесут проценты.
Конец первого периода, первоначальный депозит 50000 рублей.
Процент, первый период — 0.
Остаток, конец первого периода -50000 руб.
Процент, второго периода – 5000 руб.
Депозит, конец второго периода – 50000 руб.
Остаток, конец второго периода – 105000 руб.
Процент, конец третьего периода – 10500 руб.
Депозит, конец третьего периода – 50000 руб.
Остаток, конец третьего периода -165500 руб.
Процент, конец четвертого периода – 16500 руб.
Депозит, конец четвертого периода – 50000 руб.
Остаток, конец четвертого периода -232000 руб .
Процент, конец пятого периода – 23200 руб.
Депозит, конец пятого периода – 50000руб.
Остаток, конец пятого периода – 305200 руб.
Ответ: к концу пятого года вкладчик получит 305200 руб.
Примеры:
1) Вкладчик депонирует 25000 рублей в концекаждого года в течение 6 лет при ставке 12% и ежегодном накоплении. Какая сумма окажется к концу 6 года?
2) Вкладчик депонирует 37000 рублей в концекаждого года в течение 8 лет при ставке 14% и ежегодном накоплении. Какая сумма окажется к концу 8 года?
3) Вкладчик депонирует 18000 рублей в концекаждого года в течение 7 лет при ставке 15% и ежегодном накоплении. Какая сумма окажется к концу 7 года?
4) Вкладчик депонирует 45000 рублей в концекаждого года в течение 6 лет при ставке 18% и ежегодном накоплении. Какая сумма окажется к концу 6 года?
5) Вкладчик депонирует 51000 рублей в концекаждого года в течение 5 лет при ставке 13% и ежегодном накоплении. Какая сумма окажется к концу 5 года?
Конечную суммуFV для авансового аннуитета вычисляют после последнего внесения.
Пример 2. Вкладчик депонирует 50000 рублей в началекаждого года в течение 5 лет при ставке 10% и ежегодном накоплении. Какая сумма накопится к концу пятого года?
50000 рублей, депонированные в начале года, будут приносить проценты в течение всех последующих периодов.
Начало первого года, первоначальный депозит – 50000 рублей.
Процент, первый период – 5000 рублей.
Остаток, конец первого периода-55000 рублей.
Депозит, начало второго периода – 50000 рублей.
Процент, конец второго периода – 10500 рублей.
Остаток, конец второго периода – 60500 рублей.
Депозит, начало третьего периода – 50000 рублей.
Процент, конец третьего периода — 16500 рублей.
Остаток, конец третьего периода – 182000 рублей.
Депозит, начало четвертого периода – 50000 рублей.
Процент, конец четвертого периода – 23200 рублей.
Остаток, конец четвертого периода- 255200 рублей.
Депозит, начало пятого периода – 50000.
Процент, конец пятого периода —30520 рублей.
Остаток, конец пятого периода – 335720 рублей..
Ответ: к концу пятого года накопится 335720 рублей.
Примечание: накопления, получаемые при депонировании вкладов в начале каждого периода, могут быть рассчитаны путем сложения сумм, содержащихся в колонке приложения за весь рассматриваемый промежуток времени – 50000 * (1,1+1,21+1,331+1,4641+1,61051) = 335780 руб.
РЕПЕТИТОР ОЦЕНЩИКА
Специализированный сайт для студентов-оценщиков
Формулы сложных процентов
 Формула сложных процентов — 1 функция
Формула сложных процентов — 1 функция
Будущая стоимость денежной единицы ( FV) – накопленная сумма денежной единицы. Накопленная сумма денежной единицы показывает, какую сумму будет составлять денежная единица, вложенная сегодня, через определенный период времени при определенной ставке дисконта (доходности).
Начисление процентов 1 раз в год: FV = PV * [(1+ i ) n ] или FV = PV * кол.1
Начисление процентов чаще, чем один раз в год: FV = PV * [(1+ i / k ) nk ]
 Формула сложных процентов — 2 функция
Формула сложных процентов — 2 функция
Текущая стоимость денежной единицы ( P V) или текущая стоимость реверсии (перепродажи) показывает, какую сумму нужно иметь сегодня, чтобы через определенный период времени при определенной ставке дисконта (доходности) получить сумму, равную денежной единице, то есть какой сумме сегодня эквивалентна денежная единица, которую мы рассчитываем получить в будущем через определенный период времени.
Начисление процентов 1 раз в год: PV = FV * [1/(1+ i ) n ] или PV = FV * кол.4
Начисление процентов чаще, чем один раз в год: PV = FV * [1/(1+ i / k ) nk ]
 Формула сложных процентов — 3 функция
Формула сложных процентов — 3 функция
Текущая стоимость аннуитета показывает, какой сумме денежных средств сегодня эквивалентна серия равномерных платежей в будущем, равных одной денежной единице, за определенное количество периодов при определенной ставке дисконта.
Начисление процентов 1 раз в год: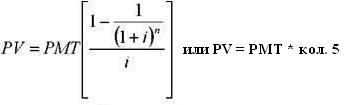
Начисление процентов чаще, чем один раз в год: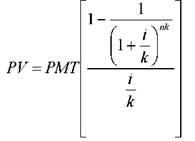
Накопление денежной единицы за период FV — будущая стоимость серии равновеликих периодических платежей (поступлений). Фактор накопления единицы за период показывает, какой будет стоимость серии равных сумм, депонированных в конце каждого периодического интервала по истечении установленного срока.
Обычный аннуитет: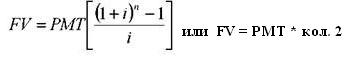
Авансовый аннуитет: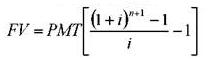
 Формула сложных процентов — 5 функция
Формула сложных процентов — 5 функция
Взнос на амортизацию денежной единицы — это величина регулярного периодического платежа в счет погашения кредита, выданного на определенный период при процентной заданной ставке. Это величина, обратная текущей стоимости аннуитета. Амортизация в данном случае – это погашение (возмещение, ликвидация) долга в течение определенного времени.
Начисление процентов чаще, чем один раз в год:
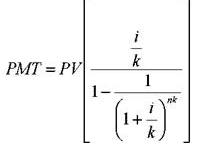
 Формула сложных процентов — 6 функция
Формула сложных процентов — 6 функция
Фактор фонда возмещения — показывает аннуитетный платеж, который необходимо депонировать под заданный процент в конце каждого периода для того, чтобы через заданное число периодов получить искомую сумму.
Начисление процентов чаще, чем один раз в год: