Функции денежной единицы
Математические основы оценочной деятельности. Шесть функций денежной единицы
Итак, для определения стоимости собственности, приносящей до ход, необходимо определить текущую стоимость денег, которые будут получены через какоето время в будущем.
Известно, а в условиях инфляции куда более очевидно, что деньги изменяют свою стоимость с течением времени. Основными операциями, позволяющими сопоставить разновременные деньги, являются операции накопления (наращивания) и дисконтирования.
Накопление – это процесс приведения текущей стоимости денег к их будущей стоимости, при условии, что вложенная сумма удерживается на счету в течение определенного времени, принося периодически нака пливаемый процент.
Дисконтирование – это процесс приведения денежных поступлений от инвестиций к их текущей стоимости.
В оценке эти финансовые расчеты базируются на сложном процессе, когда каждое последующее начисление ставки процента осуществля ется как на основную сумму, так и на начисленные за предыдущие периоды невыплаченные проценты.
Всего рассматривают шесть функций денежной единицы, основанных на сложном проценте. Для упрощения расчетов разработаны таблицы шести функций для известных ставок дохода и периода накопления ( I и n ), кроме того, можно воспользоваться финансовым калькуля тором для расчета искомой величины.
1 функция: Будущая стоимость денежной единицы (накопленная сумма денежной единицы), ( fvf , i , n ).
Если начисления осуществляются чаще, чем один раз в год, то формула преобразуется в следующую:
k – частота накоплений в год.
Данная функция используется в том случае, когда известна текущая стоимость денег и необходимо определить будущую стоимость де нежной единицы при известной ставке доходов на конец определенного периода ( n ).
Для примерного определения срока удвоения капитала (в годах) необходимо 72 разделить на целочисленное значение годовой ставки до хода на капитал. Правило действует для ставок от 3 до 18%.
Типичным примером для будущей стоимости денежной единицы может служить задача.
Определить, какая сумма будет накоплена на счете к концу 3го
года, если сегодня положить на счет, приносящий 10% годовых, 10 000
FV=10000[(1+0,1) 3 ]=13310.
2 функция : Текущая стоимость единицы (текущая стоимость реверсии (перепродажи)), ( pvf , i , n ).
Текущая стоимость единицы является обратной относительно бу дущей стоимости.
Если начисление процентов осуществляется чаще, чем один раз в год, то
Примером задачи может служить следующая: Сколько нужно вложить сегодня, чтобы к концу 5го года получить на счете 8000, если годовая ставка дохода 10%.
3 функция : Текущая стоимость аннуитета ( pvaf , i , n ).
Аннуитет – это серия равновеликих платежей (поступлений), отстоящих друг от друга на один и тот же промежуток времени.
Выделяют обычный и авансовый аннуитеты. Если платежи осуще ствляются в конце каждого периода, то аннуитет обычный, если в начале – авансовый.
Формула текущей стоимости обычного аннуитета:
PMT – равновеликие периодические платежи. Если частота начислений превышает 1 раз в год, то
Формула текущей стоимости авансового аннуитета:
Договор аренды дачи составлен на 1 год. Платежи осуществляются ежемесячно по 1000 рублей. Определить текущую стоимость аренд ных платежей при 12% ставке дисконтирования, если а) платежи осуществляются в конце месяца; б) платежи осуществляются в начале каждого месяца.
4 функция : Накопление денежной единицы за период ( fvfa , i , n ).
В результате использования данной функции определяется буду щая стоимость серии равновеликих периодических платежей (поступле ний).
Платежи также могут осуществляться в начале и в конце периода.
Формула обычного аннуитета:
Определить сумму, которая будет накоплена на счете, приносящем 12% годовых, к концу 5го года, если ежегодно откладывать на счет 10 000 рублей а) в конце каждого года; б) в начале каждого года.
5 функция : Взнос на амортизацию денежной единицы ( iaof , i , n ) Функция является обратной величиной текущей стоимости обыч ного аннуитета. Взнос на амортизацию денежной единицы используется для определения величины аннуитетного платежа в счет погашения кредита, выданного на определенный период при заданной ставке по креди ту.
Амортизация – это процесс, определяемый данной функцией, включает проценты по кредиту и оплату основной суммы долга.
При платежах, осуществляемых чаще, чем 1 раз в год используется следующая формула:
Примером может служить следующая задача: Определить, каким должны быть платежи, чтобы к концу 7го года погасить кредит в 100 000 рублей, выданный под 15% годовых.
6 функция : Фактор фонда возмещения ( sff , i , n )
Данная функция обратна функции накопления единицы за период. Фактор фонда возмещения показывает аннуитетный платеж, который необходимо депонировать под заданный процент в конце каждого пе риода для того, чтобы через заданное число периодов получить искомую сумму.
Для определения величины платежа используется формула:
При платежах (поступлениях), осуществляемых чаще, чем 1 раз в год:
Примером может служить задача.
Определить, какими должны быть платежи, чтобы к концу 5го го да иметь на счете, приносящем 12% годовых, 100 000 рублей. Платежи осуществляются в конце каждого года.
Аннуитетный платеж, определяемый данной функцией, включает выплату основной суммы без выплат процента.
РЕПЕТИТОР ОЦЕНЩИКА
Специализированный сайт для студентов-оценщиков
Формулы сложных процентов
Формула сложных процентов — 1 функция
Будущая стоимость денежной единицы ( FV) – накопленная сумма денежной единицы. Накопленная сумма денежной единицы показывает, какую сумму будет составлять денежная единица, вложенная сегодня, через определенный период времени при определенной ставке дисконта (доходности).
Начисление процентов 1 раз в год: FV = PV * [(1+ i ) n ] или FV = PV * кол.1
Начисление процентов чаще, чем один раз в год: FV = PV * [(1+ i / k ) nk ]
Формула сложных процентов — 2 функция
Текущая стоимость денежной единицы ( P V) или текущая стоимость реверсии (перепродажи) показывает, какую сумму нужно иметь сегодня, чтобы через определенный период времени при определенной ставке дисконта (доходности) получить сумму, равную денежной единице, то есть какой сумме сегодня эквивалентна денежная единица, которую мы рассчитываем получить в будущем через определенный период времени.
Начисление процентов 1 раз в год: PV = FV * [1/(1+ i ) n ] или PV = FV * кол.4
Начисление процентов чаще, чем один раз в год: PV = FV * [1/(1+ i / k ) nk ]
Формула сложных процентов — 3 функция
Текущая стоимость аннуитета показывает, какой сумме денежных средств сегодня эквивалентна серия равномерных платежей в будущем, равных одной денежной единице, за определенное количество периодов при определенной ставке дисконта.
Начисление процентов 1 раз в год: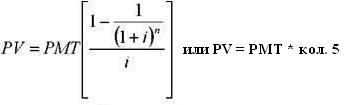
Начисление процентов чаще, чем один раз в год: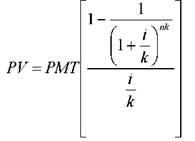
Накопление денежной единицы за период FV — будущая стоимость серии равновеликих периодических платежей (поступлений). Фактор накопления единицы за период показывает, какой будет стоимость серии равных сумм, депонированных в конце каждого периодического интервала по истечении установленного срока.
Обычный аннуитет: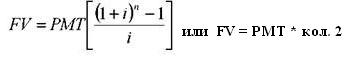
Авансовый аннуитет: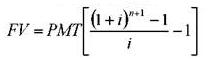
Формула сложных процентов — 5 функция
Взнос на амортизацию денежной единицы — это величина регулярного периодического платежа в счет погашения кредита, выданного на определенный период при процентной заданной ставке. Это величина, обратная текущей стоимости аннуитета. Амортизация в данном случае – это погашение (возмещение, ликвидация) долга в течение определенного времени.
Начисление процентов чаще, чем один раз в год:
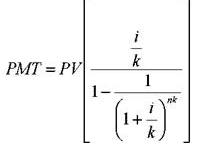
Формула сложных процентов — 6 функция
Фактор фонда возмещения — показывает аннуитетный платеж, который необходимо депонировать под заданный процент в конце каждого периода для того, чтобы через заданное число периодов получить искомую сумму.
Начисление процентов чаще, чем один раз в год: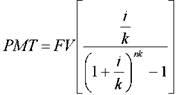
Шесть функций денежной единицы
Для определения стоимости инвестиционного проекта или собственности необходимо определить текущую стоимость денег, которые будут получены через некоторое время в будущем. В условиях инфляции деньги изменяют свою стоимость с течением времени. Основными операциями, позволяющими сопоставить разновременные деньги являются операции накопления (наращивания) и дисконтирования.
Накопление – это процесс приведения текущей стоимости денег к их будущей стоимости при условии, что вложенная сумма будет находиться на счету в течение определенного времени, принося периодически накапливаемый процент.
Дисконтирование – процесс приведения денежных поступлений от инвестиций к их текущей стоимости.
1 функция. Определим будущую стоимость денежной единицы (накопленная сумма денежных единиц)
FV — будущая стоимость денежной единицы,
PV – текущая стоимость денежной единицы,
i – ставка дохода,
n – число периодов накопления в годах.
Задача. Определить какая сумма будет накоплена на счете к концу 3 года, если сегодня положить на счет под 10 % годовых 10 тыс. руб.
2 функция. Текущая стоимость денежной единицы (текущая стоимость реверсии перепродажи)
Задача. Сколько нужно вложить сегодня в инвестиционный проект, чтобы к концу 5 года получить 8 тыс.руб. Ставка дохода 10%.
3 функция. Определение текущей стоимости аннуитета.
Аннуитет – это серия равновеликих платежей (поступлений), отстоящих друг от друга на один и тот же промежуток времени.
Выделяют обычный и авансовый аннуитет. Если платежи осуществляют в конце каждого периода, то аннуитет обычный; если вначале – авансовый.
Формула текущей стоимости обычного аннуитета:
PMT – равновеликие периодические платежи.
Задача. Договор аренды дачи составлен на 1 год. Платежи осуществляются ежемесячно по 1 тыс.руб. Определить текущую стоимость арендных платежей при 12% ставке дисконтирования. n = 12 (число периодов – месяцев).
4 функция. Накопление денежной единицы за период. В результате использования данной функции определяется будущая стоимость серии равновеликих периодических платежей или поступлений.
Задача. Определить сумму, которая будет накоплена на счете, приносящем 12% годовых, к концу 5 года, если ежегодно откладывать на счет 10 тыс.руб.
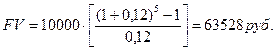
5 функция. Взнос на амортизацию денежной единицы.
Данная функция является обратной величиной текущей стоимости обычного аннуитета.
Амортизация – это процесс, определяемый данной функцией, и включает проценты по кредиту и оплату основной суммы долга.
Задача. Определить, какими должны быть ежегодные платежи, чтобы к концу 7 года погасить кредит 100 000 руб., выданный под 15% годовых.
Аннуитет может быть как поступлением (входящим денежным потоком), так и платежом (исходящим денежным потоком), по отношению к инвестору. Поэтому данная функция может быть использована в случае расчета величины равновеликого взноса на погашение кредита при известном числе взносов и заданной процентной ставке. Такой кредит называется самоамортизирующийся кредит.
6 функция. Рассматривает фактор фонда размещения и является обратной функции накопления единицы за период.
Для определения величины платежа используется следующая формула:
Задача. Определить, какими должны быть платежи, чтобы к концу 5 года иметь на счете при ставке 12% годовых 100 000 руб.
studopedia.org — Студопедия.Орг — 2014-2020 год. Студопедия не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования (0.002 с) . 
Шесть функций денежной единицы
Суть оценки стоимости приносящего прибыль проекта состоит в том, что определяется текущая стоимость прибыли, которая будет получена в прогнозируемом периоде. Гривна, полученная завтра, стоит меньше, чем гривна полученная сегодня. Это обусловлено тем, что деньги со временем приносят доход; а во-вторых — инфляционные процессы обесценивают деньги. В связи с этим рассмотрим шесть функций денежной единицы, которые отражают текущую стоимость денег.
Первая (прямая) функция. Накопление суммы денежной единицы: будущая стоимость денежной единицы.
При расчете будущей стоимости денежной единицы используется обычная формула сложного процента, которая позволяет рассчитывать и учитывать процент на вложенный процент:
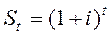, где
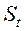– депозитная сумма после t периодов, если вложен 1 долл.; 1 – один доллар; i – периодическая ставка процента; t – число периодов.
Существую специальные таблицы шести функций денежной единицы, содержащие предварительно рассчитанные элементы (отдельные множители) сложного процента, но можно рассчитывать их и самим.
На рис. 9.1 представлена диаграмма возрастания во времени текущей стоимости, положенной на депозит, по сложному проценту.
Данные о накопленной сумме в 1 доллар по сложному проценту при ставке 10% и ежегодном накоплении.
Накопление денежных средств может происходить более часто, чем год: ежедневно. Ежемесячно, ежеквартально или каждое полугодие. При более частом накоплении денежных средств эффективная ставка снижается. Расчет производится по основной формуле сложного процента с определенной ее корректировкой: число лет (t), на протяжении которого происходит накопление, умножается на частоту накопления в течение года, а номинальная годовая ставка процента делится на частоту накопления.
Вторая (обратная) функция сложного процента: текущая стоимость денежной единицы.
Текущая стоимость денежной единицы (стоимость реверсии, V) – это величина, обратная накопленной сумме единицы:
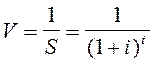
Текущая стоимость денежной единицы – это текущая стоимость одного доллара, которая будет получена в будущем. Диаграмма текущей стоимости денежной единицы показана на рис. 9.2.
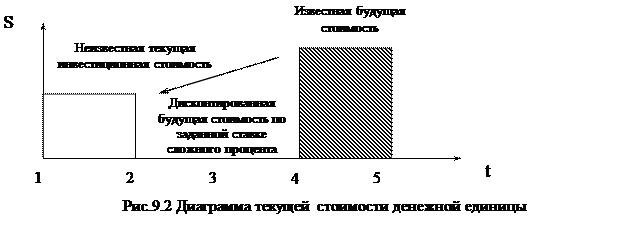
Коэффициент текущей стоимости денежной единицы используется для оценки текущей стоимости известного (или прогнозируемого) единовременного поступления денежных средств с учетом заданного процента (с учетом ставки дисконта).
Допустим, инвестору необходимо определить, сколько нужно заплатить сегодня за оцениваемое предприятие, чтобы получить от него доход в 10% годовых, а через 2 года его продать, например за 10 млн. долл. Если инвестор собирается получить 10% на вложенный капитал, то сумма, которую он может предложить за предприятие сегодня: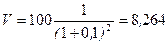 
млн. долл.
Механизм определения коэффициента текущей стоимости денежной единицы при годовой ставке дисконта 10%.
Третья (прямая) функция сложного процента: текущая стоимость единичного аннуитета.
Аннуитет (обычный) – серия равновеликих платежей, первый из которых осуществляется через один период, начиная с настоящего момента, то есть платеж производится в конце рассматриваемых периодов.
На рис.9.3 представлена диаграмма текущей стоимости обычного аннуитета, то есть текущая стоимость серии равновеликих платежей.
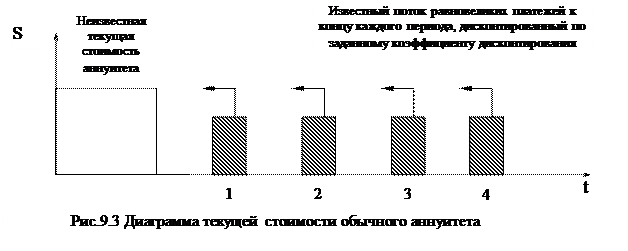
Такая ситуация может возникнуть, если собственник сдает активы предприятия в аренду и хочет получать ежегодную арендную плату в 100 тыс. долл. в течение следующих четырех лет. При 10% ставке дисконта текущая стоимость первого арендного платежа в 100 тыс. долл. через год равна 90,91 тыс. долл. (100 тыс. долл. * 0,9091=90, 91 тыс. долл.), второго арендного платежа – 82,64 тыс. долл. (100 тыс. долл. * 0,8264=82, 64 тыс. долл.), третьего арендного платежа – 75,13 тыс. долл., четвертого — 63,30 тыс. долл. Таким образом, текущая стоимость арендных платежей в 100 тыс. долл. в течение 4 последующих лет при ставке 10% составляет 316,98 тыс. долл.
Текущая стоимость аннуитета (at) может быть рассчитана как сумма текущих стоимостей 1 долл. за определенный период времени:
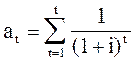
Для построения таблицы обычного аннуитета необходимо сложить данные текущей стоимости единицы за соответствующее число лет.
Если периодические платежи поступают чаще, чем один раз в год, номинальную (годовую) ставку процента необходимо разделить на число периодов в году. Общее число периодов равно числу лет, умноженному на число периодов в году.
Если собственник договаривается с арендатором о том, что он (арендатор) будет осуществлять равномерные авансовые платежи по следующей схеме: первый платеж немедленно после подписания контракта, а последующие равные платежи через определенный период, то такие платежи называются авансовым аннуитетом.
Четвертая (обратная) функция сложного процента: взнос на амортизацию денежной единицы.
Взнос на амортизацию денежной единицы – это регулярный периодический платеж в погашение кредита, приносящего процентный доход. Это величина, обратная текущей стоимости аннуитета.
Амортизация в данном случае – это погашение (возмещение, ликвидация) долга в течение определенного времени. Взнос на амортизацию кредита математически определяется как отношение одного платежа к первоначальной основной сумме кредита. Взнос на амортизацию единицы равен обязательному периодическому платежу по кредиту, включающему процент и выплату части основной суммы. Это позволяет погасить кредит и проценты по нему в течение установленного срока.
1 долл., ожидаемый к получению в конце каждого года на протяжении 4 лет, имеет при годовой ставке 10% текущую стоимость 3,1698. Это текущая стоимость аннуитета.
Величина взноса на амортизацию равна обратной величине текущей стоимости аннуитета, то есть взнос на амортизацию 1 долл. составляет величину, обратную 3,1698 долл.
Математическое отношение одного платежа к первоначальной основной сумме кредита составляет
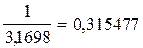
Эта величина показывает размер периодического ежегодного платежа для погашения задолженности по кредиту 3,1698 долл. в течение 4 лет при ставке 10%.
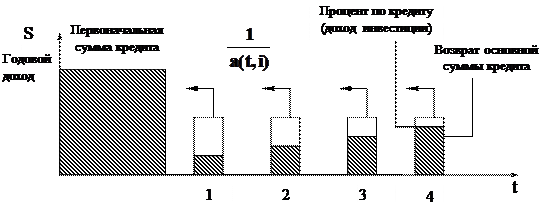Каждый взнос на амортизацию единицы включает процент и выплату части первоначальной основной суммы кредита. Соотношение этих составляющих изменяется с каждым платежом (рис. 9.4).
Рис.9.4 Взнос на амортизацию единицы
Для определения взноса на амортизацию денежной единицы используется следующая формула:
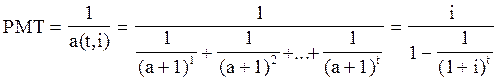
Пятая (прямая) функция сложного процента: накопление (рост) единицы за период — будущая стоимость аннуитета.
Фактор накопления единицы позволяет ответить на вопрос о том, какой по истечению всего срока будет стоимость серии равных взносов, депонированных в конце каждого из периодических интервалов.
Например, предприниматель хочет накопить определенную сумму для покупки нового станка. Станок стоит 4,641 долл. Он в конце каждого года откладывает на депозит по 1 долл., который приносит 105-ный годовой доход. К концу четвертого года он скапливает необходимую сумму (4,641 долл.) и покупает станок.
Расчет накопления единицы за период S(t,i) осуществляется по следующей формуле:
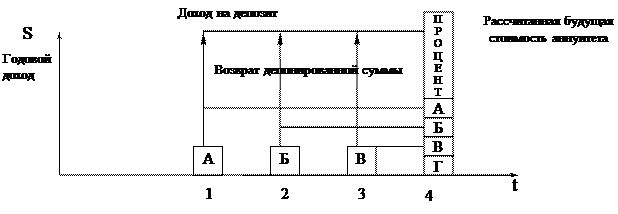
Рис.5 Накопление единицы за период
Шестая (обратная) функция сложного процента: фактор фонда возмещения.
Фактор фонда возмещения показывает сумму, которую нужно депонировать в конце каждого периода (периодический депозит), чтобы через заданное число периодов остаток на счете составил 1 долл. При этом учитывается процент, получаемый по депозитам.
Например, предпринимателю необходимо за четыре года скопить 4,641 долл. для покупки станка. Какие суммы денег ему необходимо откладывать каждый год при 10% годовых, чтобы через 4 года купить этот станок?
Ответ: ежегодный вклад должен составить 1 долл. (0,215471*4,641=1 долл.).
Фактор фонда возмещения – это величина обратная фактору накопления денежной единицы за период:
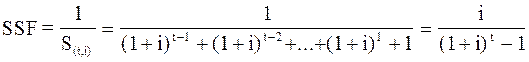
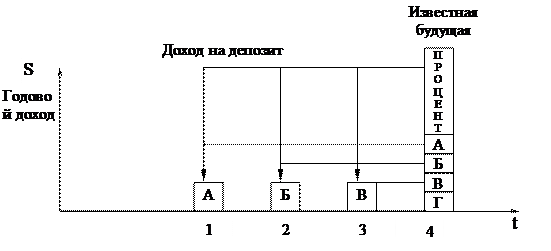
Рис.5 Фактор фонда возмещения
Взаимосвязи между функциями сложного процента.
Все шесть функций сложного процента строятся с использованием общей базовой формулы сложного процента (1+i) t , характеризующей накопленную сумму единицы. Все пять функций сложного процента являются производными от первой (прямой) функции сложного процента – накопленной функции единицы (будущая стоимость единицы). Каждая из функций предполагает, что деньги положенные на депозит, до тех пор, пока находятся на нем, приносят процент. В основу каждого фактора положен эффект сложного процента, при котором процент переводится в основную сумму (табл.9.2).
Таблица 9.2 Взаимосвязь между функциями сложного процента
